Inverse Hyperbolic Cosine
Calculator for calculating the angle to the inverse hyperbolic cosine
ACosh Calculator
Domain Restriction
The ACosh(x) or inverse hyperbolic cosine shows inverse function behavior with domain x ≥ 1.
ACosh Function Curve
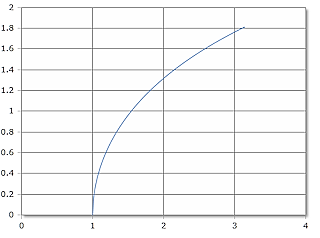
The ACosh function starts at (1,0) and increases logarithmically.
Domain: [1, ∞), Range: [0, ∞)
|
|
Inverse Function Behavior of ACosh
The inverse hyperbolic cosine function exhibits characteristic inverse properties:
- Domain: [1, ∞) (x ≥ 1)
- Range: [0, ∞) (non-negative angles)
- Starting Point: ACosh(1) = 0
- Inverse: Cosh(ACosh(x)) = x for x ≥ 1
- Monotonicity: Strictly increasing
- Growth: Logarithmic growth rate
Logarithmic Representation of ACosh Function
The inverse hyperbolic cosine function is expressed through logarithmic functions:
Basic Formula
Natural logarithm expression for x ≥ 1
Inverse Relation
For x ≥ 1
Formulas for the ACosh Function
Definition
Natural logarithm expression for x ≥ 1
Inverse Relation
Fundamental inverse function properties
Derivative
First derivative for x > 1
Domain Restriction
Returns NaN for x < 1
Asymptotic Behavior
Logarithmic growth for large arguments
Special Values
Important Values
Invalid Input
Function undefined for x < 1
Starting Point
Function starts at the point (1, 0)
Properties
- Inverse function
- Strictly increasing
- Logarithmic growth
- Domain restricted to x ≥ 1
Growth Rate
Logarithmic growth pattern
Applications
Relativistic physics, hyperbolic geometry, engineering calculations, inverse problems.
Detailed Description of the ACosh Function
Definition and Input
The inverse hyperbolic cosine function ACosh(x) is the inverse function of the hyperbolic cosine. It exhibits characteristic logarithmic growth with a restricted domain.
Input
The argument must be greater than or equal to 1. If the value is less than 1, the function returns NaN (not a valid number).
Result
The result is given in degrees (full circle = 360°) or radians (full circle = 2π). The unit of measurement used is set using the Degrees or Radians menu.
Using the Calculator
Enter a value greater than or equal to 1. The ACosh function calculates the angle that corresponds to the value of the hyperbolic cosine.
Mathematical Properties
Function Properties
- Domain: [1, ∞) (x ≥ 1)
- Range: [0, ∞) (non-negative)
- Starting Point: ACosh(1) = 0
- Monotonicity: Strictly increasing
Inverse Properties
- Inverse of hyperbolic cosine function
- Undoes the effect of Cosh for x ≥ 1
- Returns the original angle for Cosh values
- One-to-one correspondence with Cosh
Applications
- Relativistic Physics: Rapidity calculations
- Hyperbolic Geometry: Distance measurements
- Engineering: Catenary problems
- Mathematics: Inverse hyperbolic problems
Practical Notes
- Domain restriction: x ≥ 1 (undefined for x < 1)
- Starting value: ACosh(1) = 0
- Logarithmic growth: ACosh(x) ≈ ln(2x) for large x
- Inverse relation: Cosh(ACosh(x)) = x for x ≥ 1
Calculation Examples
Basic Values
ACosh(1) = 0
ACosh(2) ≈ 1.317
ACosh(3) ≈ 1.763
Special Values
ACosh(e) ≈ 1.657
ACosh(5) ≈ 2.292
ACosh(10) ≈ 2.993
Invalid Inputs
ACosh(0) = NaN
ACosh(0.5) = NaN
x < 1: undefined
Physical and Mathematical Applications
Relativistic Physics
Rapidity Calculation:
φ = ACosh(γ)
Where γ is the Lorentz factor
Application: Converting between energy and rapidity.
Hyperbolic Geometry
Distance Formula:
d = ACosh(1 + 2·sinh²(r/2))
Hyperbolic distance calculations
Example: Non-Euclidean geometry applications.
Important Mathematical Relationships
Inverse Function Properties
Identities: Fundamental inverse relationships.
Calculus Properties
Derivative: Involves square root in denominator.
|
|
|
|