Inverse Hyperbolic Cosecant

Online calculator for calculating the angle to the inverse hyperbolic cosecant

ACsch Calculator

Zero Exclusion

The ACsch(x) or inverse hyperbolic cosecant shows inverse function behavior with domain x ≠ 0.

Value can be positive or negative, but not zero
Results
Angle:
Complex Numbers

You can find the ACsch function for calculating a complex number here

ACsch Function Curve

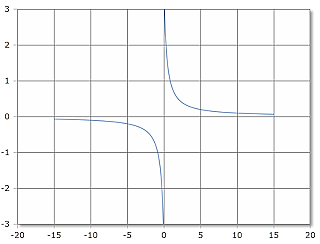
Curve of the ACsch function

The ACsch function has two separate branches with a pole at x = 0.
Domain: ℝ \ {0}, Range: ℝ

Inverse Function Behavior of ACsch

The inverse hyperbolic cosecant function exhibits characteristic inverse properties:

  • Domain: ℝ \ {0} (all real numbers except 0)
  • Range: ℝ (all real numbers)
  • Singularity: Pole at x = 0
  • Inverse: Csch(ACsch(x)) = x for x ≠ 0
  • Symmetry: Odd function ACsch(-x) = -ACsch(x)
  • Branches: Two continuous branches

Logarithmic Representation of ACsch Function

The inverse hyperbolic cosecant function is expressed through logarithmic functions:

Basic Formula
\[\text{ACsch}(x) = \ln\left(\frac{1}{x} + \sqrt{\frac{1}{x^2} + 1}\right)\]

Natural logarithm expression for x ≠ 0

Inverse Relation
\[\text{csch}(\text{ACsch}(x)) = x\]

For x ≠ 0

Formulas for the ACsch Function

Definition
\[\text{ACsch}(x) = \ln\left(\frac{1}{x} + \sqrt{\frac{1}{x^2} + 1}\right)\]

Natural logarithm expression for x ≠ 0

Alternative Form
\[\text{ACsch}(x) = \ln\left(\frac{1 + \sqrt{1 + x^2}}{|x|}\right) \cdot \text{sgn}(x)\]

Alternative logarithmic representation

Derivative
\[\frac{d}{dx} \text{ACsch}(x) = -\frac{1}{|x|\sqrt{1 + x^2}}\]

First derivative for x ≠ 0

Symmetry Property
\[\text{ACsch}(-x) = -\text{ACsch}(x)\]

Odd function (antisymmetric)

Limit Behavior
\[\lim_{x \to 0^+} \text{ACsch}(x) = +\infty\] \[\lim_{x \to 0^-} \text{ACsch}(x) = -\infty\] \[\lim_{x \to \pm\infty} \text{ACsch}(x) = 0\]

Pole at origin and asymptotic behavior

Special Values

Important Values
ACsch(1) ≈ 0.881 ACsch(-1) ≈ -0.881 ACsch(2) ≈ 0.481
Singularity
\[x = 0: \text{∞}\]

Function has a pole at x = 0

Asymptotic Behavior
\[\text{ACsch}(x) \approx \frac{1}{x} \text{ for large } |x|\]

Approaches zero as x approaches ±∞

Properties
  • Inverse function
  • Odd function symmetry
  • Pole at origin
  • Two continuous branches
Zero Behavior
\[\lim_{x \to \pm\infty} \text{ACsch}(x) = 0\]

Horizontal asymptote at y = 0

Applications

Signal processing, inverse problems, mathematical physics, numerical analysis.

Detailed Description of the ACsch Function

Definition and Input

The inverse hyperbolic cosecant function ACsch(x) is the inverse function of the hyperbolic cosecant. It exhibits characteristic pole behavior with a singularity at the origin.

Critical Property: The ACsch function has a pole at x = 0!
Input

The argument can be a positive or negative number. If 0 is entered, the result is ∞ (infinity).

Result

The result is given in degrees (full circle = 360°) or radians (full circle = 2π). The unit of measurement used is set using the Degrees or Radians menu.

Using the Calculator

Enter any non-zero value. The ACsch function calculates the angle whose hyperbolic cosecant equals the input value.

Mathematical Properties

Function Properties
  • Domain: ℝ \ {0} (all real numbers except 0)
  • Range: ℝ (all real numbers)
  • Singularity: Pole at x = 0
  • Symmetry: Odd function ACsch(-x) = -ACsch(x)
Pole Properties
  • Vertical asymptote at x = 0
  • Approaches +∞ as x → 0⁺
  • Approaches -∞ as x → 0⁻
  • Two continuous branches separated by pole
Applications
  • Signal Processing: Inverse transformations
  • Mathematical Physics: Singular solutions
  • Numerical Analysis: Pole handling
  • Engineering: Reciprocal system analysis
Practical Notes
  • Pole at x = 0: Function diverges to ±∞
  • Odd function: ACsch(-x) = -ACsch(x)
  • Inverse relation: Csch(ACsch(x)) = x for x ≠ 0
  • Asymptotic approach to zero for large |x|

Calculation Examples

Small Values

ACsch(0.1) ≈ 2.993

ACsch(0.5) ≈ 1.444

ACsch(1) ≈ 0.881

Negative Values

ACsch(-0.1) ≈ -2.993

ACsch(-1) ≈ -0.881

ACsch(-2) ≈ -0.481

Limit Behavior

x → 0⁺: ACsch(x) → +∞

x → 0⁻: ACsch(x) → -∞

x → ±∞: ACsch(x) → 0

Mathematical and Physical Applications

Signal Processing

Inverse Transforms:

Reciprocal signal recovery

Pole-based filtering

Application: Inverse cosecant transforms in communications.

Numerical Analysis

Pole Handling:

Singular point analysis

Reciprocal function inverses

Example: Handling singularities in computational methods.

Important Mathematical Relationships

Inverse Function Properties
\[\text{csch}(\text{ACsch}(x)) = x \text{ for } x \neq 0\] \[\text{ACsch}(\text{csch}(y)) = y \text{ for } y \neq 0\]

Identities: Fundamental inverse relationships.

Calculus Properties
\[\frac{d}{dx}\text{ACsch}(x) = -\frac{1}{|x|\sqrt{1+x^2}}\] \[\int \text{ACsch}(x) dx = x\text{ACsch}(x) + \text{sgn}(x)\sqrt{1+x^2} + C\]

Derivative: Involves absolute value and square root.


IT Functions

Decimal, Hex, Bin, Octal conversion • Shift bits left or right • Set a bit • Clear a bit • Bitwise AND • Bitwise OR • Bitwise exclusive OR

Special functions

Airy • Derivative Airy • Bessel-I • Bessel-Ie • Bessel-J • Bessel-Je • Bessel-K • Bessel-Ke • Bessel-Y • Bessel-Ye • Spherical-Bessel-J • Spherical-Bessel-Y • Hankel • Beta • Incomplete Beta • Incomplete Inverse Beta • Binomial Coefficient • Binomial Coefficient Logarithm • Erf • Erfc • Erfi • Erfci • Fibonacci • Fibonacci Tabelle • Gamma • Inverse Gamma • Log Gamma • Digamma • Trigamma • Logit • Sigmoid • Derivative Sigmoid • Softsign • Derivative Softsign • Softmax • ReLU • Softplus • Swish • Struve • Struve table • Modified Struve • Modified Struve table • Riemann Zeta

Hyperbolic functions

ACosh • ACoth • ACsch • ASech • ASinh • ATanh • Cosh • Coth • Csch • Sech • Sinh • Tanh

Trigonometrische Funktionen

ACos • ACot • ACsc • ASec • ASin • ATan • Cos • Cot • Csc • Sec • Sin • Sinc • Tan • Degree to Radian • Radian to Degree