ATan - Arctangent (Inverse Tangent)
Online calculator for calculating the angle to the tangent
Arctangent Calculator
Instructions
Enter the value of the tangent (any real number), select the unit of measure (degrees or radians) and click Calculate.
Arctangent - Overview
Value Range
The arctangent accepts all real numbers as input.
- Domain: All real numbers (-∞, +∞)
- Range: (-π/2, π/2) in radians or (-90°, 90°)
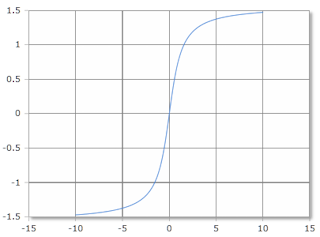
Inverse tangent, scale in radians
Definition
The arctangent (arctan, atan, or tan⁻¹) is the inverse function of the tangent function.
\(\displaystyle y = \arctan(x) \Leftrightarrow \tan(y) = x \)
with \( x \in \mathbb{R} \) and \( y \in \left(-\frac{\pi}{2}, \frac{\pi}{2}\right) \)
Alternative Notation
\(\displaystyle \text{arctan}(x) = \tan^{-1}(x) = \text{atan}(x) \)
|
|
Description of the Arctangent
Fundamentals
The arctangent (also known as arctan or tan⁻¹) is a mathematical function that serves as the inverse function of the tangent. It helps find the angle whose tangent corresponds to a given number. The arctangent function is closely related to the tangent function and plays a significant role in mathematics, especially in trigonometry and complex function theory.
Mathematical Definition:
\(\displaystyle y = \arctan(x) \)
means
\(\displaystyle \tan(y) = x \)
Understanding Tangent
In a right triangle, the tangent of an angle α is the ratio of the opposite side to the adjacent side:
\(\displaystyle \tan(\alpha) = \frac{\text{Opposite}}{\text{Adjacent}} = \frac{a}{b} \)
Also: \(\displaystyle \tan(\alpha) = \frac{\sin(\alpha)}{\cos(\alpha)} \)
Important: The range of arctangent is \( -\frac{\pi}{2} < y < \frac{\pi}{2} \), ensuring a unique angle for each input.
Detailed Examples
Example 1: Calculate Tangent Value
Given:
A right triangle with:
- Opposite side: a = 3
- Adjacent side: b = 4
Calculating the tangent:
\(\displaystyle \tan(\alpha) = \frac{3}{4} = 0.75 \)
Example 2: Calculate Angle
Task:
Calculate the angle α for \( \tan(\alpha) = 0.75 \)
In radians:
\(\displaystyle \alpha = \arctan(0.75) \approx 0.6435 \text{ rad} \)
Conversion to degrees:
\(\displaystyle \alpha = \frac{0.6435 \cdot 180°}{\pi} \approx 36.87° \)
Example 3: Special Values
Common tangent values:
- \( \arctan(0) = 0° = 0 \text{ rad} \)
- \( \arctan(1) = 45° = \frac{\pi}{4} \text{ rad} \)
- \( \arctan(\sqrt{3}) = 60° = \frac{\pi}{3} \text{ rad} \)
- \( \arctan(\infty) = 90° = \frac{\pi}{2} \text{ rad} \) (limit)
Conversion Formula
From radians to degrees:
\(\displaystyle \text{Degrees} = \frac{\text{Radians} \cdot 180°}{\pi} \)
Properties
- Domain: \( x \in \mathbb{R} \) (all real numbers)
- Range: \( y \in \left(-\frac{\pi}{2}, \frac{\pi}{2}\right) \) (radians) or \( (-90°, 90°) \)
- Monotonicity: Strictly monotonically increasing
- Symmetry: Odd function: \( \arctan(-x) = -\arctan(x) \)
- Asymptotes: Horizontal asymptotes at \( y = \pm\frac{\pi}{2} \)
- Special values:
- \( \arctan(0) = 0 \)
- \( \arctan(1) = \frac{\pi}{4} = 45° \)
- \( \arctan(-1) = -\frac{\pi}{4} = -45° \)
Practical Applications
- Geometry: Angle calculations in triangles
- Engineering: Structural analysis and design
- Physics: Projectile motion and optics
- Navigation: Direction and bearing calculations
- Computer graphics: Rotation and orientation
- Signal processing: Phase angle calculations
- Robotics: Inverse kinematics
Relationships to Other Functions
Tangent relationship:
\(\displaystyle \tan(\arctan(x)) = x \)
\(\displaystyle \arctan(\tan(x)) = x \)
for \( x \in \left(-\frac{\pi}{2}, \frac{\pi}{2}\right) \)
Derivative:
\(\displaystyle \frac{d}{dx}\arctan(x) = \frac{1}{1+x^2} \)
Series expansion:
\(\displaystyle \arctan(x) = \sum_{n=0}^{\infty}\frac{(-1)^n x^{2n+1}}{2n+1} \)
Useful Identities
\(\displaystyle \arctan(x) + \arctan\left(\frac{1}{x}\right) = \frac{\pi}{2} \)
for \( x > 0 \)
\(\displaystyle \arctan(a) + \arctan(b) = \arctan\left(\frac{a+b}{1-ab}\right) \)
for \( ab < 1 \)
Important Note
Notation: The notation tan⁻¹(x) can be confusing as it might be mistaken for the reciprocal function (1/tan(x)), which is actually the cotangent (cot(x)). In programming and mathematical software, use atan or arctan.
Two-argument form: Many programming languages also provide atan2(y, x), which considers the signs of both arguments to determine the correct quadrant of the angle. This is useful for converting Cartesian coordinates (x, y) to polar coordinates.
|
|