Hyperbolic Secant

Online calculator for calculating the hyperbolic secant of an angle

Sech Calculator

Universal Domain

The Sech(x) or hyperbolic secant shows bell curve behavior for all real numbers.

Enter any angle value in degrees or radians
Results
Sech:

Sech Function Curve

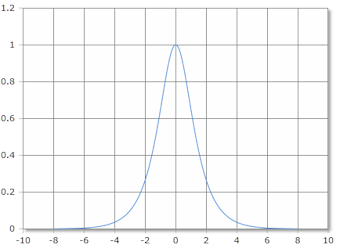
Curve of the Sech function

The Sech function forms a bell curve with maximum value 1 at x = 0.
Domain: ℝ, Range: (0, 1]

Bell Curve Behavior of Sech

The hyperbolic secant function exhibits characteristic bell curve properties:

  • Domain: ℝ (all real numbers)
  • Range: (0, 1] (values between 0 and 1)
  • Maximum: Sech(0) = 1
  • Reciprocal: Sech(x) = 1/Cosh(x)
  • Symmetry: Even function Sech(-x) = Sech(x)
  • Shape: Classic bell curve (soliton profile)

Exponential Representation of Sech Function

The hyperbolic secant function is expressed through exponential functions:

Basic Formula
\[\text{Sech}(x) = \frac{1}{\cosh(x)} = \frac{2}{e^x + e^{-x}}\]

Reciprocal of hyperbolic cosine

Soliton Relation
\[u(x) = A \cdot \text{sech}(kx)\]

Classic soliton pulse shape

Formulas for the Sech Function

Definition
\[\text{Sech}(x) = \frac{1}{\cosh(x)} = \frac{2}{e^x + e^{-x}}\]

Reciprocal of hyperbolic cosine for all x ∈ ℝ

Soliton Equation
\[u(x,t) = A \cdot \text{sech}(k(x - vt))\]

Traveling wave solution (soliton pulse)

Derivative
\[\frac{d}{dx} \text{Sech}(x) = -\text{Sech}(x) \cdot \text{Tanh}(x)\]

Derivative involves both secant and tangent

Symmetry Property
\[\text{Sech}(-x) = \text{Sech}(x)\]

Even function (symmetric about y-axis)

Asymptotic Behavior
\[\lim_{x \to \pm\infty} \text{Sech}(x) = 0\] \[\text{Sech}(0) = 1\]

Bell curve with maximum at origin

Special Values

Important Values
Sech(0) = 1 Sech(1) ≈ 0.648 Sech(ln(2)) = 0.8
Universal Domain
\[x \in \mathbb{R} \text{ (all real numbers)}\]

Function defined everywhere

Maximum Value
\[\text{Sech}(x) \leq 1\]

Maximum value is 1 at x = 0

Properties
  • Even function
  • Bell curve shape
  • Bounced between 0 and 1
  • Soliton profile
Reciprocal Relation
\[\text{Sech}(x) \cdot \text{Cosh}(x) = 1\]

Perfect reciprocal of hyperbolic cosine

Applications

Soliton theory, nonlinear optics, signal processing, probability theory.

Detailed Description of the Sech Function

Definition and Input

The hyperbolic secant function Sech(x) is the reciprocal of the hyperbolic cosine function. It exhibits characteristic bell curve behavior and is fundamental in soliton theory and nonlinear wave physics.

Key Advantage: The Sech function is bounded and bell-shaped!
Input

The angle is given in degrees (full circle = 360°) or radians (full circle = 2π). The unit of measurement used is set using the Degrees or Radians menu. All real numbers are valid inputs.

Result

The result is always between 0 and 1, with the maximum value of 1 occurring at x = 0. The function decreases exponentially as |x| increases.

Using the Calculator

Enter any angle value. The Sech function calculates the hyperbolic secant, which represents the classic soliton pulse shape.

Mathematical Properties

Function Properties
  • Domain: ℝ (all real numbers)
  • Range: (0, 1] (bounded positive values)
  • Maximum: Sech(0) = 1
  • Symmetry: Even function Sech(-x) = Sech(x)
Bell Curve Properties
  • Classic bell shape (soliton profile)
  • Maximum at origin, decreasing symmetrically
  • Exponential decay for large arguments
  • Bounded between 0 and 1
Applications
  • Soliton Theory: Pulse propagation in optical fibers
  • Nonlinear Optics: Self-focusing phenomena
  • Signal Processing: Pulse shape analysis
  • Probability Theory: Bell-shaped distributions
Practical Notes
  • No domain restrictions: accepts any real number
  • Bounded output: 0 < Sech(x) ≤ 1 for all x
  • Even function: Sech(-x) = Sech(x)
  • Bell shape: Classic soliton pulse profile

Calculation Examples

Central Values

Sech(0) = 1

Sech(1) ≈ 0.648

Sech(2) ≈ 0.266

Special Values

Sech(ln(2)) = 0.8

Sech(ln(3)) ≈ 0.6

Sech(π) ≈ 0.086

Large Arguments

Sech(5) ≈ 0.0135

Sech(10) ≈ 9.1e-5

Exponential decay

Soliton and Nonlinear Applications

Soliton Theory

Pulse Shape:

u(x,t) = A·Sech(k(x-vt))

Self-preserving wave pulse

Application: Optical fiber communication systems.

Nonlinear Optics

Self-Focusing:

Kerr effect in optical media

Bright soliton solutions

Example: Pulse propagation in nonlinear crystals.

Important Mathematical Relationships

Reciprocal Function Properties
\[\text{Sech}(x) = \frac{1}{\cosh(x)}\] \[\text{Sech}(x) \cdot \cosh(x) = 1\]

Reciprocal Relationship: Perfect inverse of hyperbolic cosine.

Calculus Properties
\[\frac{d}{dx}\text{Sech}(x) = -\text{Sech}(x)\text{Tanh}(x)\] \[\int \text{Sech}(x) dx = \arctan(\sinh(x)) + C\]

Derivative: Product of secant and tangent.


IT Functions

Decimal, Hex, Bin, Octal conversion • Shift bits left or right • Set a bit • Clear a bit • Bitwise AND • Bitwise OR • Bitwise exclusive OR

Special functions

Airy • Derivative Airy • Bessel-I • Bessel-Ie • Bessel-J • Bessel-Je • Bessel-K • Bessel-Ke • Bessel-Y • Bessel-Ye • Spherical-Bessel-J • Spherical-Bessel-Y • Hankel • Beta • Incomplete Beta • Incomplete Inverse Beta • Binomial Coefficient • Binomial Coefficient Logarithm • Erf • Erfc • Erfi • Erfci • Fibonacci • Fibonacci Tabelle • Gamma • Inverse Gamma • Log Gamma • Digamma • Trigamma • Logit • Sigmoid • Derivative Sigmoid • Softsign • Derivative Softsign • Softmax • Struve • Struve table • Modified Struve • Modified Struve table • Riemann Zeta

Hyperbolic functions

ACosh • ACoth • ACsch • ASech • ASinh • ATanh • Cosh • Coth • Csch • Sech • Sinh • Tanh

Trigonometrische Funktionen

ACos • ACot • ACsc • ASec • ASin • ATan • Cos • Cot • Csc • Sec • Sin • Sinc • Tan • Degree to Radian • Radian to Degree