Sec - Calculate Secant
Online calculator for calculating the secant of an angle
Secant Calculator
Instructions
Enter the angle whose secant you want to calculate, select the unit of measure (degrees or radians) and click Calculate.
Secant - Overview
Value Range
The angle is given in degrees (full circle = 360°) or radians (full circle = 2·π).
Note: The secant is undefined at 90°, 270° (or π/2, 3π/2 in radians) where cos(α) = 0.
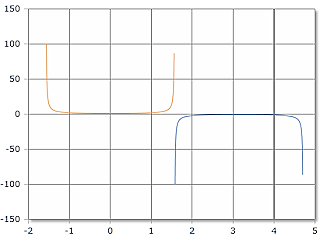
Secant, scale in radians
Definition in Triangle
The secant is the reciprocal of the cosine function. In a right triangle, it is the ratio of the hypotenuse to the adjacent side.
\(\displaystyle \sec(\alpha) = \frac{\text{Hypotenuse}}{\text{Adjacent}} = \frac{c}{b} = \frac{1}{\cos(\alpha)} \)

Important Values
- \( \sec(0°) = 1 \)
- \( \sec(30°) = \frac{2}{\sqrt{3}} \approx 1.155 \)
- \( \sec(45°) = \sqrt{2} \approx 1.414 \)
- \( \sec(60°) = 2 \)
- \( \sec(90°) = \) undefined (∞)
- \( \sec(180°) = -1 \)
|
|
Description of the Secant
Fundamentals
The secant (sec) is one of the six basic trigonometric functions. It is the reciprocal of the cosine function. In a right triangle, the secant of an angle α is the ratio of the hypotenuse to the adjacent side.
Definition:
\(\displaystyle \sec(\alpha) = \frac{\text{Hypotenuse}}{\text{Adjacent}} = \frac{c}{b} \)
\(\displaystyle \sec(\alpha) = \frac{1}{\cos(\alpha)} \)
Properties
The secant function has several important properties:
- Periodic: sec(α + 360°) = sec(α)
- Even function: sec(-α) = sec(α)
- Undefined: At 90°, 270°, ... (where cos(α) = 0)
- Range: (-∞, -1] ∪ [1, +∞)
- Domain: All real numbers except 90° + n·180° (n integer)
Relationship to Other Functions
The secant is related to other trigonometric functions:
\(\displaystyle \sec(\alpha) = \frac{1}{\cos(\alpha)} \)
\(\displaystyle \cos(\alpha) = \frac{1}{\sec(\alpha)} \)
\(\displaystyle 1 + \tan^2(\alpha) = \sec^2(\alpha) \)
Detailed Examples
Example 1: Calculate Secant
Given:
A right triangle with:
- Hypotenuse: \( c = 10 \text{ cm} \)
- Adjacent side: \( b = 8 \text{ cm} \)
Calculation:
\(\displaystyle \sec(\alpha) = \frac{10}{8} = 1.25 \)
To find the angle: \( \alpha = \arccos\left(\frac{8}{10}\right) \approx 36.87° \)
Example 2: Known Angles
Important secant values:
| \( \sec(0°) \) | = | 1 |
| \( \sec(30°) \) | = | \( \frac{2}{\sqrt{3}} \approx 1.155 \) |
| \( \sec(45°) \) | = | \( \sqrt{2} \approx 1.414 \) |
| \( \sec(60°) \) | = | 2 |
| \( \sec(120°) \) | = | -2 |
| \( \sec(180°) \) | = | -1 |
Example 3: Using Cosine
Task:
If \( \cos(\alpha) = 0.5 \), what is \( \sec(\alpha) \)?
Solution:
\(\displaystyle \sec(\alpha) = \frac{1}{\cos(\alpha)} = \frac{1}{0.5} = 2 \)
This corresponds to α = 60° (or π/3 rad)
Conversion
From degrees to radians:
\(\displaystyle \text{Radians} = \frac{\text{Degrees} \cdot \pi}{180°} \)
Mathematical Properties
- Period: 360° or 2π (radians)
- Symmetry: Even function: sec(-α) = sec(α)
- Asymptotes: Vertical at 90°, 270°, ...
- Minimum value: |sec(α)| ≥ 1
- Reciprocal: sec(α) = 1/cos(α)
- Pythagorean identity: 1 + tan²(α) = sec²(α)
- Relationship to arccosine:
- \( \text{arcsec}(x) = \arccos\left(\frac{1}{x}\right) \)
Practical Applications
- Physics: Wave analysis and optics
- Engineering: Structural mechanics calculations
- Navigation: Distance and bearing calculations
- Astronomy: Angular measurements
- Surveying: Slope and grade calculations
- Cryptography: Mathematical algorithms
- Computer graphics: 3D transformations
- Mathematics: Solving trigonometric equations
Important Note
The secant function is undefined at angles where the cosine equals zero (90°, 270°, ... or π/2, 3π/2, ...). At these points, the function approaches positive or negative infinity. The secant is the reciprocal of the cosine: sec(α) = 1/cos(α). Since |cos(α)| ≤ 1, the absolute value of the secant is always ≥ 1: |sec(α)| ≥ 1. The function has a period of 360° (or 2π radians), meaning sec(α + 360°) = sec(α). The secant function is particularly useful in calculus and in solving trigonometric equations, and it plays an important role in the Pythagorean identity: 1 + tan²(α) = sec²(α).
|
|