Sinc - Kardinalsinus berechnen
Online Rechner zur Berechnung des Kardinalsinus (Spaltfunktion)
Kardinalsinus Rechner
Anleitung
Geben Sie den Winkel ein, dessen Kardinalsinus berechnet werden soll, wählen Sie die Maßeinheit (Grad oder Radiant) und klicken Sie auf Rechnen.
Kardinalsinus - Übersicht
Wichtiger Hinweis
Der Kardinalsinus (auch Spaltfunktion oder si-Funktion) existiert in zwei Varianten: normiert und nichtnormiert. Hier wird die nichtnormierte Variante berechnet.
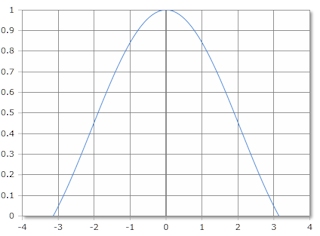
Kardinalsinus, Skala in Radiant
Nichtnormierte Variante
Die nichtnormierte Kardinalsinus-Funktion ist definiert als:
\(\displaystyle \text{sinc}(x) = \begin{cases} \frac{\sin(x)}{x} & \text{für } x \neq 0 \\ 1 & \text{für } x = 0 \end{cases} \)
Normierte Variante
In der Signalverarbeitung wird oft die normierte Form verwendet:
\(\displaystyle \text{sinc}(x) = \frac{\sin(\pi x)}{\pi x} \)
|
|
Beschreibung zum Kardinalsinus
Grundlagen
Der Kardinalsinus (lateinisch: sinus cardinalis, auch si-Funktion oder Spaltfunktion) ist eine analytische Funktion, die in der Signalverarbeitung, Optik und Informationstheorie wichtig ist.
Nichtnormierte Definition:
\(\displaystyle \text{sinc}(x) = \frac{\sin(x)}{x} \quad \text{für } x \neq 0 \)
\(\displaystyle \text{sinc}(0) = 1 \)
(Grenzwert: \( \lim_{x \to 0} \frac{\sin(x)}{x} = 1 \))
Eigenschaften
Die Kardinalsinus-Funktion hat mehrere wichtige Eigenschaften:
- Gerade Funktion: sinc(-x) = sinc(x)
- Maximum bei x = 0: sinc(0) = 1
- Nullstellen: Bei x = n·π (n ≠ 0, ganzzahlig)
- Asymptotisches Verhalten: sinc(x) → 0 für x → ±∞
- Oszillierend: Gedämpfte Schwingungen
Zwei Varianten
Es gibt zwei gebräuchliche Definitionen:
1. Nichtnormiert (hier verwendet):
\(\displaystyle \text{sinc}(x) = \frac{\sin(x)}{x} \)
2. Normiert (Signalverarbeitung):
\(\displaystyle \text{sinc}(x) = \frac{\sin(\pi x)}{\pi x} \)
Detailliertes Beispiel
Beispiel 1: Berechnung bei x = 0
Aufgabe:
Berechnen Sie sinc(0).
Lösung:
Bei x = 0 würde die Formel sin(0)/0 zu 0/0 führen. Wir verwenden den Grenzwert:
\(\displaystyle \lim_{x \to 0} \frac{\sin(x)}{x} = 1 \)
\(\displaystyle \therefore \text{sinc}(0) = 1 \)
Beispiel 2: Berechnung bei x = π
Aufgabe:
Berechnen Sie sinc(π).
Berechnung:
\(\displaystyle \text{sinc}(\pi) = \frac{\sin(\pi)}{\pi} = \frac{0}{\pi} = 0 \)
Dies ist eine Nullstelle der Funktion.
Beispiel 3: Nullstellen
Nullstellen der Funktion:
Die Kardinalsinus-Funktion hat Nullstellen bei:
\(\displaystyle x = n \cdot \pi, \quad n = \pm 1, \pm 2, \pm 3, ... \)
Also bei: ±π, ±2π, ±3π, ±4π, ...
Umrechnung
Von Grad zu Radiant:
\(\displaystyle \text{Radiant} = \frac{\text{Grad} \cdot \pi}{180°} \)
Mathematische Eigenschaften
- Symmetrie: Gerade Funktion: sinc(-x) = sinc(x)
- Wertebereich: -0.217 ≤ sinc(x) ≤ 1
- Maximum: sinc(0) = 1
- Nullstellen: Bei x = n·π (n ≠ 0)
- Nebenmaxima: Bei x ≈ ±4.49, ±7.73, ... (gedämpft)
- Grenzwert: \( \lim_{x \to \infty} \text{sinc}(x) = 0 \)
- Integral: \( \int_{-\infty}^{\infty} \text{sinc}(x) \, dx = \pi \)
- Fourier-Transform: Rechteckfunktion im Frequenzbereich
Praktische Anwendungen
- Signalverarbeitung: Idealer Tiefpassfilter (Rekonstruktion)
- Optik: Beugungsmuster am Einzelspalt (Fraunhofer-Beugung)
- Informationstheorie: Shannon-Abtasttheorem
- Bildverarbeitung: Interpolation und Resampling
- Akustik: Lautsprechereigenschaften
- Radar/Sonar: Impulsformung
- Kommunikationstechnik: Pulsformung
- Astronomie: Teleskopauflösung
Wichtiger Hinweis
Die Kardinalsinus-Funktion ist besonders wichtig in der Signalverarbeitung, da sie die Impulsantwort eines idealen Tiefpassfilters darstellt. Die Funktion ist bei x = 0 stetig, obwohl die Formel dort nicht direkt anwendbar ist - der Grenzwert ergibt sinc(0) = 1. Die Fourier-Transformierte der Kardinalsinus-Funktion ist eine Rechteckfunktion, was sie zum theoretischen Idealfilter macht. In der Praxis wird sie für Signalrekonstruktion nach dem Shannon-Abtasttheorem verwendet. Beachten Sie, dass es zwei Definitionen gibt: die nichtnormierte (hier implementiert) mit Nullstellen bei n·π, und die normierte mit Nullstellen bei ganzen Zahlen n.
|
|