Cos - Calculate Cosine
Online calculator for calculating the cosine of an angle
Cosine Calculator
Instructions
Enter the angle whose cosine you want to calculate, select the unit of measure (degrees or radians) and click Calculate.
Cosine - Overview
Value Range
The angle is given in degrees (full circle = 360°) or radians (full circle = 2·π). The result always lies in the range from -1 to +1.
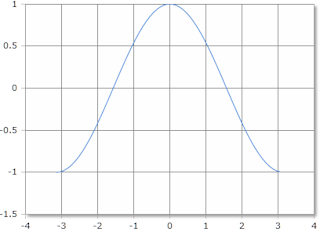
Cosine, scale in radians
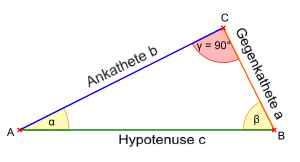
Definition in Triangle
The cosine of an angle α corresponds to the ratio of the adjacent side to the hypotenuse in a right triangle.
\(\displaystyle \cos(\alpha) = \frac{\text{Adjacent}}{\text{Hypotenuse}} = \frac{b}{c} \)
Important Values
- \( \cos(0°) = 1 \)
- \( \cos(30°) = \frac{\sqrt{3}}{2} \approx 0.866 \)
- \( \cos(45°) = \frac{\sqrt{2}}{2} \approx 0.707 \)
- \( \cos(60°) = 0.5 \)
- \( \cos(90°) = 0 \)
- \( \cos(180°) = -1 \)
|
|
Description of the Cosine
Fundamentals
The cosine is one of the fundamental trigonometric functions. In a right triangle, the cosine of an angle α is the ratio of the adjacent side to the hypotenuse.
Definition:
\(\displaystyle \cos(\alpha) = \frac{\text{Adjacent}}{\text{Hypotenuse}} \)
\(\displaystyle \cos(\alpha) = \frac{b}{c} \)
Properties
The cosine function has several important properties:
- Periodic: cos(α + 360°) = cos(α)
- Even function: cos(-α) = cos(α)
- Range: -1 ≤ cos(α) ≤ 1
- Domain: All real numbers
Relationship to Sine
Cosine and sine are closely related:
\(\displaystyle \cos(\alpha) = \sin(90° - \alpha) \)
\(\displaystyle \sin^2(\alpha) + \cos^2(\alpha) = 1 \)
Detailed Examples
Example 1: Calculate Cosine
Given:
A right triangle with:
- Adjacent side (to α): \( b = 8 \text{ cm} \)
- Hypotenuse: \( c = 10 \text{ cm} \)
Calculation:
\(\displaystyle \cos(\alpha) = \frac{8}{10} = 0.8 \)
To find the angle: \( \alpha = \arccos(0.8) \approx 36.87° \)
Example 2: Known Angles
Important cosine values:
| \( \cos(0°) \) | = | 1 |
| \( \cos(30°) \) | = | \( \frac{\sqrt{3}}{2} \approx 0.866 \) |
| \( \cos(45°) \) | = | \( \frac{\sqrt{2}}{2} \approx 0.707 \) |
| \( \cos(60°) \) | = | 0.5 |
| \( \cos(90°) \) | = | 0 |
| \( \cos(180°) \) | = | -1 |
Example 3: Practical Application
Task:
A ladder leans against a wall at an angle of 60°. The ladder is 5 m long. How far is the base of the ladder from the wall?
Solution:
\(\displaystyle \text{Distance} = 5 \cdot \cos(60°) = 5 \cdot 0.5 = 2.5 \text{ m} \)
Conversion
From degrees to radians:
\(\displaystyle \text{Radians} = \frac{\text{Degrees} \cdot \pi}{180°} \)
Mathematical Properties
- Period: 360° or 2π (radians)
- Symmetry: Even function: cos(-α) = cos(α)
- Zeros: At 90° + n·180° (n integer)
- Extrema:
- Maximum: 1 at 0°, 360°, 720°, ...
- Minimum: -1 at 180°, 540°, ...
- Addition formulas:
- \( \cos(\alpha + \beta) = \cos\alpha\cos\beta - \sin\alpha\sin\beta \)
- \( \cos(\alpha - \beta) = \cos\alpha\cos\beta + \sin\alpha\sin\beta \)
Practical Applications
- Physics: Calculation of force components
- Navigation: Course calculations and positioning
- Civil engineering: Static calculations and structures
- Astronomy: Calculation of celestial positions
- Computer graphics: 3D rotations and transformations
- Electrical engineering: AC current calculations
- Mechanical engineering: Motion analysis and kinematics
- Surveying: Distance and height calculations
Important Note
The cosine is a periodic function with a period of 360° or 2π. This means that cos(α) = cos(α + 360°). The range always lies between -1 and +1, regardless of the input angle. The cosine function is an even function, i.e., symmetric about the y-axis: cos(-α) = cos(α). Together with sine, the cosine satisfies the fundamental trigonometric identity: sin²(α) + cos²(α) = 1, known as the Pythagorean identity.
|
|