Inverse Hyperbolic Sine

Online calculator for calculating the angle to the inverse hyperbolic sine

ASinh Calculator

Unrestricted Domain

The ASinh(x) or inverse hyperbolic sine shows inverse function behavior for all real numbers.

Value can be any positive or negative real number
Results
Angle:

ASinh Function Curve

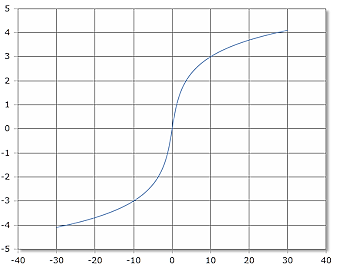
Curve of the ASinh function

The ASinh function is defined for all real numbers and is strictly increasing.
Domain: ℝ, Range: ℝ

Inverse Function Behavior of ASinh

The inverse hyperbolic sine function exhibits characteristic inverse properties:

  • Domain: ℝ (all real numbers)
  • Range: ℝ (all real numbers)
  • Zero Point: ASinh(0) = 0
  • Inverse: Sinh(ASinh(x)) = x for all x
  • Symmetry: Odd function ASinh(-x) = -ASinh(x)
  • Monotonicity: Strictly increasing

Logarithmic Representation of ASinh Function

The inverse hyperbolic sine function is expressed through logarithmic functions:

Basic Formula
\[\text{ASinh}(x) = \ln(x + \sqrt{x^2 + 1})\]

Natural logarithm expression for all x ∈ ℝ

Inverse Relation
\[\sinh(\text{ASinh}(x)) = x\]

For all x ∈ ℝ

Formulas for the ASinh Function

Definition
\[\text{ASinh}(x) = \ln(x + \sqrt{x^2 + 1})\]

Natural logarithm expression for all x ∈ ℝ

Inverse Relation
\[\sinh(\text{ASinh}(x)) = x \text{ for all } x \in \mathbb{R}\] \[\text{ASinh}(\sinh(y)) = y \text{ for all } y \in \mathbb{R}\]

Perfect inverse function properties

Derivative
\[\frac{d}{dx} \text{ASinh}(x) = \frac{1}{\sqrt{x^2 + 1}}\]

First derivative for all x ∈ ℝ

Symmetry Property
\[\text{ASinh}(-x) = -\text{ASinh}(x)\]

Odd function (antisymmetric)

Asymptotic Behavior
\[\text{ASinh}(x) \approx \ln(2|x|) \cdot \text{sgn}(x) \text{ for large } |x|\]

Logarithmic growth for large arguments

Special Values

Important Values
ASinh(0) = 0 ASinh(1) ≈ 0.881 ASinh(-1) ≈ -0.881
Unrestricted Domain
\[x \in \mathbb{R} \text{ (all real numbers)}\]

Function defined everywhere

Zero Point
\[\text{ASinh}(0) = 0\]

Function passes through origin

Properties
  • Inverse function
  • Strictly increasing
  • Odd function symmetry
  • Unrestricted domain
Growth Pattern
\[\text{ASinh}(x) \sim \ln(x) \text{ as } x \to +\infty\] \[\text{ASinh}(x) \sim -\ln(-x) \text{ as } x \to -\infty\]

Logarithmic growth pattern

Applications

Relativistic physics, engineering calculations, signal processing, mathematical modeling.

Detailed Description of the ASinh Function

Definition and Input

The inverse hyperbolic sine function ASinh(x) is the inverse function of the hyperbolic sine. It exhibits characteristic unrestricted domain behavior, making it the most versatile inverse hyperbolic function.

Key Advantage: The ASinh function accepts any real number as input!
Input

The argument can be a positive or negative number. There are no domain restrictions - all real numbers are valid inputs.

Result

The result is given in degrees (full circle = 360°) or radians (full circle = 2π). The unit of measurement used is set using the Degrees or Radians menu.

Using the Calculator

Enter any real number. The ASinh function calculates the angle whose hyperbolic sine equals the input value.

Mathematical Properties

Function Properties
  • Domain: ℝ (all real numbers)
  • Range: ℝ (all real numbers)
  • Zero Point: ASinh(0) = 0
  • Symmetry: Odd function ASinh(-x) = -ASinh(x)
Unrestricted Properties
  • No domain restrictions or singularities
  • Continuous and differentiable everywhere
  • Perfect inverse of Sinh function
  • Logarithmic growth for large arguments
Applications
  • Relativistic Physics: Velocity calculations
  • Engineering: Cable and chain problems
  • Signal Processing: Amplitude transformations
  • Mathematical Modeling: Growth processes
Practical Notes
  • No domain restrictions: accepts any real number
  • Origin passage: ASinh(0) = 0
  • Odd function: ASinh(-x) = -ASinh(x)
  • Perfect inverse: Sinh(ASinh(x)) = x for all x

Calculation Examples

Small Values

ASinh(0) = 0

ASinh(0.5) ≈ 0.481

ASinh(1) ≈ 0.881

Negative Values

ASinh(-0.5) ≈ -0.481

ASinh(-1) ≈ -0.881

ASinh(-2) ≈ -1.444

Large Values

ASinh(10) ≈ 2.993

ASinh(100) ≈ 5.298

Logarithmic growth

Mathematical and Physical Applications

Relativistic Physics

Velocity Addition:

v = c · tanh(ASinh(v₁/c) + ASinh(v₂/c))

Relativistic velocity composition

Application: Calculating combined relativistic velocities.

Engineering Applications

Catenary Problems:

Cable tension analysis

Chain and rope calculations

Example: Suspension bridge cable shape analysis.

Important Mathematical Relationships

Perfect Inverse Properties
\[\sinh(\text{ASinh}(x)) = x \text{ for all } x \in \mathbb{R}\] \[\text{ASinh}(\sinh(y)) = y \text{ for all } y \in \mathbb{R}\]

Perfect Inverse: No domain restrictions on either side.

Calculus Properties
\[\frac{d}{dx}\text{ASinh}(x) = \frac{1}{\sqrt{x^2+1}}\] \[\int \text{ASinh}(x) dx = x\text{ASinh}(x) - \sqrt{x^2+1} + C\]

Derivative: Always positive, ensuring strict monotonicity.


IT Functions

Decimal, Hex, Bin, Octal conversion • Shift bits left or right • Set a bit • Clear a bit • Bitwise AND • Bitwise OR • Bitwise exclusive OR

Special functions

Airy • Derivative Airy • Bessel-I • Bessel-Ie • Bessel-J • Bessel-Je • Bessel-K • Bessel-Ke • Bessel-Y • Bessel-Ye • Spherical-Bessel-J • Spherical-Bessel-Y • Hankel • Beta • Incomplete Beta • Incomplete Inverse Beta • Binomial Coefficient • Binomial Coefficient Logarithm • Erf • Erfc • Erfi • Erfci • Fibonacci • Fibonacci Tabelle • Gamma • Inverse Gamma • Log Gamma • Digamma • Trigamma • Logit • Sigmoid • Derivative Sigmoid • Softsign • Derivative Softsign • Softmax • Struve • Struve table • Modified Struve • Modified Struve table • Riemann Zeta

Hyperbolic functions

ACosh • ACoth • ACsch • ASech • ASinh • ATanh • Cosh • Coth • Csch • Sech • Sinh • Tanh

Trigonometrische Funktionen

ACos • ACot • ACsc • ASec • ASin • ATan • Cos • Cot • Csc • Sec • Sin • Sinc • Tan • Degree to Radian • Radian to Degree