Hyperbolic Cosine

Online calculator for calculating the hyperbolic cosine of an angle

Cosh Calculator

Universal Domain

The Cosh(x) or hyperbolic cosine shows catenary curve behavior for all real numbers.

Enter any angle value in degrees or radians
Results
Cosh:

Cosh Function Curve

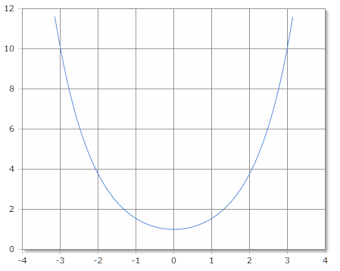
Curve of the Cosh function

The Cosh function forms a catenary curve with minimum value 1 at x = 0.
Domain: ℝ, Range: [1, ∞)

Catenary Curve Behavior of Cosh

The hyperbolic cosine function exhibits characteristic catenary properties:

  • Domain: ℝ (all real numbers)
  • Range: [1, ∞) (values ≥ 1)
  • Minimum: Cosh(0) = 1
  • Symmetry: Even function Cosh(-x) = Cosh(x)
  • Growth: Exponential for large |x|
  • Shape: Classic catenary curve

Exponential Representation of Cosh Function

The hyperbolic cosine function is expressed through exponential functions:

Basic Formula
\[\text{Cosh}(x) = \frac{e^x + e^{-x}}{2}\]

Average of exponential and its reciprocal

Catenary Relation
\[y = a \cdot \cosh\left(\frac{x}{a}\right)\]

Hanging chain equation

Formulas for the Cosh Function

Definition
\[\text{Cosh}(x) = \frac{e^x + e^{-x}}{2}\]

Exponential average for all x ∈ ℝ

Catenary Equation
\[y = a \cdot \cosh\left(\frac{x}{a}\right)\]

Shape of hanging cables and chains

Derivative
\[\frac{d}{dx} \text{Cosh}(x) = \text{Sinh}(x)\]

Derivative is hyperbolic sine

Symmetry Property
\[\text{Cosh}(-x) = \text{Cosh}(x)\]

Even function (symmetric about y-axis)

Hyperbolic Identity
\[\text{Cosh}^2(x) - \text{Sinh}^2(x) = 1\]

Fundamental hyperbolic identity

Special Values

Important Values
Cosh(0) = 1 Cosh(1) ≈ 1.543 Cosh(ln(2)) = 1.25
Universal Domain
\[x \in \mathbb{R} \text{ (all real numbers)}\]

Function defined everywhere

Minimum Value
\[\text{Cosh}(x) \geq 1\]

Minimum value is 1 at x = 0

Properties
  • Even function
  • Always positive
  • Catenary curve shape
  • Exponential growth
Growth Pattern
\[\text{Cosh}(x) \approx \frac{e^{|x|}}{2} \text{ for large } |x|\]

Exponential growth for large arguments

Applications

Engineering (cables, chains), architecture, physics, mathematical modeling.

Detailed Description of the Cosh Function

Definition and Input

The hyperbolic cosine function Cosh(x) is defined as the average of exponential functions. It exhibits characteristic catenary curve behavior representing the shape of hanging cables and chains.

Key Advantage: The Cosh function accepts any real number and is always positive!
Input

The angle is given in degrees (full circle = 360°) or radians (full circle = 2π). The unit of measurement used is set using the Degrees or Radians menu.

Result

The result is always greater than or equal to 1, with the minimum value occurring at x = 0. The function grows exponentially for large positive or negative arguments.

Using the Calculator

Enter any angle value. The Cosh function calculates the hyperbolic cosine, which represents the catenary curve equation.

Mathematical Properties

Function Properties
  • Domain: ℝ (all real numbers)
  • Range: [1, ∞) (values ≥ 1)
  • Minimum: Cosh(0) = 1
  • Symmetry: Even function Cosh(-x) = Cosh(x)
Catenary Properties
  • Represents shape of hanging cables and chains
  • Minimum energy configuration under gravity
  • U-shaped curve with vertex at (0, 1)
  • Exponential growth for large arguments
Applications
  • Engineering: Cable and chain calculations
  • Architecture: Arch and bridge design
  • Physics: Wave equations and relativity
  • Mathematics: Special relativity and geometry
Practical Notes
  • No domain restrictions: accepts any real number
  • Always positive: Cosh(x) ≥ 1 for all x
  • Even function: Cosh(-x) = Cosh(x)
  • Catenary shape: Natural curve of hanging objects

Calculation Examples

Basic Values

Cosh(0) = 1

Cosh(1) ≈ 1.543

Cosh(2) ≈ 3.762

Special Values

Cosh(ln(2)) = 1.25

Cosh(ln(3)) ≈ 1.667

Cosh(π) ≈ 11.592

Large Arguments

Cosh(5) ≈ 74.21

Cosh(10) ≈ 11013.2

Exponential growth

Engineering and Physical Applications

Catenary Engineering

Cable Shape:

y = a·Cosh(x/a)

Natural shape of hanging cables

Application: Bridge design, power lines, suspension structures.

Wave Physics

Wave Solutions:

ψ(x,t) = A·Cosh(kx)·e^(-iωt)

Evanescent wave solutions

Example: Quantum tunneling, electromagnetic waves.

Important Mathematical Relationships

Hyperbolic Identity
\[\cosh^2(x) - \sinh^2(x) = 1\] \[\cosh(x + y) = \cosh(x)\cosh(y) + \sinh(x)\sinh(y)\]

Fundamental Identity: Analogous to trigonometric identity.

Calculus Properties
\[\frac{d}{dx}\cosh(x) = \sinh(x)\] \[\int \cosh(x) dx = \sinh(x) + C\]

Derivative: Derivative is hyperbolic sine.


IT Functions

Decimal, Hex, Bin, Octal conversion • Shift bits left or right • Set a bit • Clear a bit • Bitwise AND • Bitwise OR • Bitwise exclusive OR

Special functions

Airy • Derivative Airy • Bessel-I • Bessel-Ie • Bessel-J • Bessel-Je • Bessel-K • Bessel-Ke • Bessel-Y • Bessel-Ye • Spherical-Bessel-J • Spherical-Bessel-Y • Hankel • Beta • Incomplete Beta • Incomplete Inverse Beta • Binomial Coefficient • Binomial Coefficient Logarithm • Erf • Erfc • Erfi • Erfci • Fibonacci • Fibonacci Tabelle • Gamma • Inverse Gamma • Log Gamma • Digamma • Trigamma • Logit • Sigmoid • Derivative Sigmoid • Softsign • Derivative Softsign • Softmax • Struve • Struve table • Modified Struve • Modified Struve table • Riemann Zeta

Hyperbolic functions

ACosh • ACoth • ACsch • ASech • ASinh • ATanh • Cosh • Coth • Csch • Sech • Sinh • Tanh

Trigonometrische Funktionen

ACos • ACot • ACsc • ASec • ASin • ATan • Cos • Cot • Csc • Sec • Sin • Sinc • Tan • Degree to Radian • Radian to Degree