ACsc - Arkuskosekans (inverser Kosekans)
Online Rechner zur Berechnung des Arkuskosekans (inverser Kosekans)
Arkuskosekans Rechner
Anleitung
Geben Sie den Wert des Kosekans ein (|x| ≥ 1), wählen Sie die Maßeinheit (Grad oder Radiant) und klicken Sie auf Rechnen.
Arkuskosekans - Übersicht
Wertebereich Eingabe
Der Wert des Arguments muss |x| ≥ 1 sein, d.h. x ≤ -1 oder x ≥ 1. Das Resultat wird in Grad (-90° bis +90°) oder Radiant (-π/2 bis +π/2) angegeben.
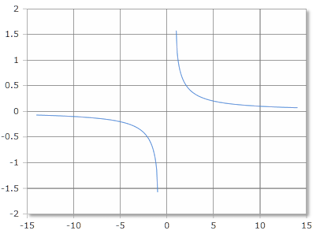
Inverser Kosekans, Skala in Radiant
Definition
Der Arkuskosekans (arccsc, acsc oder csc⁻¹) ist die Umkehrfunktion der Kosekans-Funktion. Sie berechnet den Winkel für einen gegebenen Kosekanswert.
\(\displaystyle y = \text{arccsc}(x) \Leftrightarrow \csc(y) = x \)
mit \( |x| \geq 1 \) und \( y \in [-\frac{\pi}{2}, \frac{\pi}{2}] \), \( y \neq 0 \)
Beziehung zum Sinus
Der Kosekans ist der Kehrwert des Sinus:
\(\displaystyle \csc(\alpha) = \frac{1}{\sin(\alpha)} \)
|
|
Beschreibung zum Arkuskosekans
Grundlagen
Die inverse Kosekansfunktion, bezeichnet als arccsc, acsc oder csc⁻¹, ist die Umkehrfunktion der Kosekans-Funktion. Sie wird verwendet, um den Winkel zu einem gegebenen Kosekanswert zu berechnen.
Mathematische Definition:
\(\displaystyle y = \text{arccsc}(x) \)
bedeutet
\(\displaystyle \csc(y) = x \)
Kosekans im rechtwinkligen Dreieck
In einem rechtwinkligen Dreieck ist der Kosekans eines Winkels α das Verhältnis der Hypotenuse zur Gegenkathete:
\(\displaystyle \csc(\alpha) = \frac{\text{Hypotenuse}}{\text{Gegenkathete}} = \frac{c}{a} \)
\(\displaystyle \csc(\alpha) = \frac{1}{\sin(\alpha)} \)
Beziehung zum Sinus
Der Kosekans ist der Kehrwert des Sinus:
\(\displaystyle \csc(\alpha) = \frac{1}{\sin(\alpha)} \)
\(\displaystyle \sin(\alpha) = \frac{1}{\csc(\alpha)} \)
Detailliertes Beispiel
Beispiel 1: Kosekanswert berechnen
Gegeben:
Ein rechtwinkliges Dreieck mit:
- Hypotenuse: \( c = 10 \)
- Gegenkathete: \( a = 6 \)
Berechnung des Kosekans:
\(\displaystyle \csc(\alpha) = \frac{10}{6} \approx 1.667 \)
Beispiel 2: Winkel berechnen
Aufgabe:
Berechnen Sie den Winkel α für \( \csc(\alpha) = 1.667 \)
In Radiant:
\(\displaystyle \alpha = \text{arccsc}(1.667) \approx 0.644 \text{ rad} \)
Umrechnung in Grad:
\(\displaystyle \alpha = \frac{0.644 \cdot 180°}{\pi} \approx 36.87° \)
Beispiel 3: Mit Sinus
Alternative Berechnung:
Da \( \csc(\alpha) = \frac{1}{\sin(\alpha)} \):
\(\displaystyle \sin(\alpha) = \frac{1}{1.667} \approx 0.6 \)
\(\displaystyle \alpha = \arcsin(0.6) \approx 36.87° \)
Formel zur Umrechnung
Von Bogenmaß in Grad:
\(\displaystyle \text{Grad} = \frac{\text{Radiant} \cdot 180°}{\pi} \)
Eigenschaften
- Definitionsbereich: \( |x| \geq 1 \) (x ≤ -1 oder x ≥ 1)
- Wertebereich: \( y \in [-\frac{\pi}{2}, \frac{\pi}{2}] \), \( y \neq 0 \) oder [-90°, 90°] ohne 0°
- Monotonie: Auf jedem Intervall streng monoton fallend
- Spezielle Werte:
- \( \text{arccsc}(1) = \frac{\pi}{2} \approx 90° \)
- \( \text{arccsc}(-1) = -\frac{\pi}{2} \approx -90° \)
- \( \text{arccsc}(2) \approx 30° \)
- \( \text{arccsc}(\sqrt{2}) \approx 45° \)
Praktische Anwendungen
- Geometrie: Berechnung von Winkeln in speziellen Dreiecken
- Trigonometrie: Lösung trigonometrischer Gleichungen
- Physik: Wellenberechnung und Schwingungsanalyse
- Navigation: Astronomische Berechnungen
- Ingenieurwesen: Strukturanalyse und Statik
- Signalverarbeitung: Fourier-Analyse
Wichtige Formeln
Sinus und Kosekans:
\(\displaystyle \sin(\alpha) = \frac{\text{Gegenkathete}}{\text{Hypotenuse}} = \frac{a}{c} \)
\(\displaystyle \csc(\alpha) = \frac{\text{Hypotenuse}}{\text{Gegenkathete}} = \frac{c}{a} \)
Kehrwertbeziehung:
\(\displaystyle \csc(\alpha) = \frac{1}{\sin(\alpha)} \)
\(\displaystyle \sin(\alpha) = \frac{1}{\csc(\alpha)} \)
Beziehung zum Arkussinus:
\(\displaystyle \text{arccsc}(x) = \arcsin\left(\frac{1}{x}\right) \quad \text{für } |x| \geq 1 \)
Wichtiger Hinweis
Beachten Sie, dass der Kosekans nur für Werte |x| ≥ 1 definiert ist, da der Sinus im Bereich [-1, 1] liegt. Der Arkuskosekans kann nicht für Werte zwischen -1 und 1 berechnet werden. Der Wertebereich des Arkuskosekans schließt den Wert 0 aus, da der Kosekans bei 0° bzw. 0 rad nicht definiert ist.
|
|