ATan - Arkustangens (inverser Tangens)
Online Rechner zur Berechnung des Winkels zum Tangens
Arkustangens Rechner
Anleitung
Geben Sie den Wert des Tangens ein (beliebige reelle Zahl), wählen Sie die Maßeinheit (Grad oder Radiant) und klicken Sie auf Rechnen.
Arkustangens - Übersicht
Wertebereich
Der Eingabewert kann jede reelle Zahl sein. Das Resultat wird in Grad (-90° bis +90°) oder Bogenmaß/Radiant (-π/2 bis +π/2) angegeben.
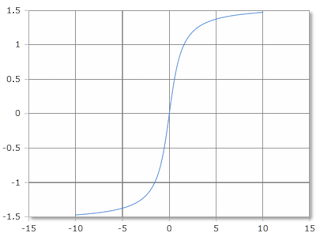
Inverser Tangens, Skala in Radiant
Definition
Der Arkustangens (arctan, atan oder tan⁻¹) ist die Umkehrfunktion der Tangens-Funktion. Sie berechnet den Winkel für einen gegebenen Tangenswert.
\(\displaystyle y = \arctan(x) \Leftrightarrow \tan(y) = x \)
mit \( x \in \mathbb{R} \) und \( y \in (-\frac{\pi}{2}, \frac{\pi}{2}) \) (Radiant)
Umrechnung
Von Bogenmaß zu Grad:
\(\displaystyle \text{Grad} = \frac{\text{Radiant} \cdot 180°}{\pi} \)
|
|
Beschreibung zum Arkustangens
Grundlagen
Der Arkustangens (auch bekannt als arctan, atan oder tan⁻¹) ist die Umkehrfunktion der Tangens-Funktion. Er hilft, den Winkel zu finden, dessen Tangens einer bestimmten Zahl entspricht.
Mathematische Definition:
\(\displaystyle y = \arctan(x) \)
bedeutet
\(\displaystyle \tan(y) = x \)
Tangens im rechtwinkligen Dreieck
In einem rechtwinkligen Dreieck ist der Tangens eines Winkels α das Verhältnis der Gegenkathete zur Ankathete:
\(\displaystyle \tan(\alpha) = \frac{\text{Gegenkathete}}{\text{Ankathete}} = \frac{a}{b} \)
\(\displaystyle \tan(\alpha) = \frac{\sin(\alpha)}{\cos(\alpha)} \)
Besonderheit
Der Arkustangens kann jeden reellen Zahlenwert als Eingabe akzeptieren, im Gegensatz zum Arkussinus und Arkuskosinus, die auf [-1, 1] beschränkt sind.
\(\displaystyle \lim_{x \to \infty} \arctan(x) = \frac{\pi}{2} \approx 90° \)
\(\displaystyle \lim_{x \to -\infty} \arctan(x) = -\frac{\pi}{2} \approx -90° \)
Detailliertes Beispiel
Beispiel 1: Tangenswert berechnen
Gegeben:
Ein rechtwinkliges Dreieck mit:
- Gegenkathete: \( a = 3 \)
- Ankathete: \( b = 4 \)
Berechnung des Tangens:
\(\displaystyle \tan(\alpha) = \frac{3}{4} = 0.75 \)
Beispiel 2: Winkel berechnen
Aufgabe:
Berechnen Sie den Winkel α für \( \tan(\alpha) = 0.75 \)
In Radiant:
\(\displaystyle \alpha = \arctan(0.75) \approx 0.6435 \text{ rad} \)
Umrechnung in Grad:
\(\displaystyle \alpha = \frac{0.6435 \cdot 180°}{\pi} \approx 36.87° \)
Beispiel 3: Bekannte Werte
Häufig verwendete Tangenswerte:
- \( \arctan(0) = 0° \)
- \( \arctan(1) = 45° \) (gleichschenkliges Dreieck)
- \( \arctan(\sqrt{3}) \approx 60° \)
- \( \arctan(\frac{1}{\sqrt{3}}) \approx 30° \)
Formel zur Umrechnung
Von Bogenmaß in Grad:
\(\displaystyle \text{Grad} = \frac{\text{Radiant} \cdot 180°}{\pi} \)
Eigenschaften
- Definitionsbereich: \( x \in \mathbb{R} \) (alle reellen Zahlen)
- Wertebereich: \( y \in (-\frac{\pi}{2}, \frac{\pi}{2}) \) oder (-90°, 90°)
- Monotonie: Streng monoton steigend
- Spezielle Werte:
- \( \arctan(0) = 0° \)
- \( \arctan(1) = 45° \)
- \( \arctan(-1) = -45° \)
- \( \arctan(\sqrt{3}) \approx 60° \)
- Grenzwerte:
- \( \lim_{x \to \infty} \arctan(x) = 90° \)
- \( \lim_{x \to -\infty} \arctan(x) = -90° \)
Praktische Anwendungen
- Navigation: Berechnung von Peilungswinkeln und Kursen
- Computergrafik: 2D/3D-Rotationen und Kameraausrichtung
- Robotik: Inverse Kinematik und Wegplanung
- Physik: Wurfparabeln und Geschwindigkeitsvektoren
- Ingenieurwesen: Steigungen und Neigungswinkel
- Signalverarbeitung: Phasenwinkelberechnung
Wichtiger Hinweis
Der Arkustangens ist eng mit der Tangensfunktion verwandt und spielt eine bedeutende Rolle in der Mathematik, insbesondere in der Theorie komplexer Funktionen und der Trigonometrie. Er ist neben den Arkuskosinus- und Arkussinusfunktionen eine der Kernfunktionen in der Klasse der Arkusfunktionen. Im Gegensatz zum Arkussinus und Arkuskosinus kann der Arkustangens jeden reellen Zahlenwert als Eingabe akzeptieren, wobei der Ausgabewert immer zwischen -90° und +90° liegt.
|
|