Tan - Tangens berechnen
Onlinerechner zur Berechnung des Tangens eines Winkels
Tangens Rechner
Anleitung
Geben Sie den Winkel ein, dessen Tangens berechnet werden soll, wählen Sie die Maßeinheit (Grad oder Radiant) und klicken Sie auf Rechnen.
Tangens - Übersicht
Wertebereich
Der Winkel kann in Grad (>-90° ... <90°) oder Bogenmaß/Radiant (>-π/2 ... <π/2) angegeben werden. Der Tangens ist bei ±90° bzw. ±π/2 nicht definiert.
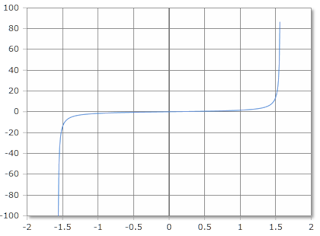
Tangens, Skala in Radiant
Definition im rechtwinkligen Dreieck
Der Tangens eines Winkels entspricht dem Verhältnis von Gegenkathete zu Ankathete in einem rechtwinkligen Dreieck.
\(\displaystyle \tan(\alpha) = \frac{\text{Gegenkathete}}{\text{Ankathete}} = \frac{a}{b} \)
Alternative Definition
Der Tangens kann auch durch Sinus und Kosinus ausgedrückt werden:
\(\displaystyle \tan(\alpha) = \frac{\sin(\alpha)}{\cos(\alpha)} \)
|
|
Beschreibung zum Tangens
Grundlagen
Der Tangens (tan oder tg) ist eine der grundlegenden trigonometrischen Funktionen. In einem rechtwinkligen Dreieck entspricht der Tangens dem Verhältnis der Gegenkathete zur Ankathete. Die Tangens-Funktion berechnet hier den Tangens eines Winkels, der als reelle Zahl in Grad oder Radiant angegeben wird.
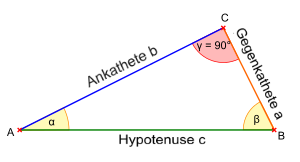
Mathematische Definition:
\(\displaystyle \tan(\alpha) = \frac{a}{b} \)
wobei a die Gegenkathete und b die Ankathete ist
Beziehung zu Sinus und Kosinus
Der Tangens kann auch durch das Verhältnis von Sinus zu Kosinus definiert werden:
\(\displaystyle \tan(\alpha) = \frac{\sin(\alpha)}{\cos(\alpha)} \)
Wichtig: Der Tangens ist bei ±90° (bzw. ±π/2) nicht definiert, da an diesen Stellen der Kosinus gleich Null ist und eine Division durch Null nicht möglich ist.
Detaillierte Beispiele
Beispiel 1: Tangens im Dreieck
Gegeben:
Ein rechtwinkliges Dreieck mit:
- Gegenkathete: \( a = 3 \) cm
- Ankathete: \( b = 4 \) cm
Berechnung:
\(\displaystyle \tan(\alpha) = \frac{a}{b} = \frac{3}{4} = 0.75 \)
Beispiel 2: Tangens für 45°
Berechnung:
\(\displaystyle \tan(45°) = \tan\left(\frac{\pi}{4}\right) = 1 \)
Bei 45° sind Gegenkathete und Ankathete gleich lang, daher ist der Tangens = 1.
Beispiel 3: Steigungswinkel
Aufgabe:
Eine Straße hat eine Steigung von 10%. Wie groß ist der Steigungswinkel?
Lösung:
10% Steigung bedeutet: \( \tan(\alpha) = 0.10 \)
\(\displaystyle \tan(\alpha) = 0.10 \)
\(\displaystyle \alpha = \arctan(0.10) \approx 5.71° \)
Umrechnung
Von Grad in Bogenmaß:
\(\displaystyle \text{Radiant} = \frac{\text{Grad} \cdot \pi}{180°} \)
Von Bogenmaß in Grad:
\(\displaystyle \text{Grad} = \frac{\text{Radiant} \cdot 180°}{\pi} \)
Eigenschaften
- Definitionsbereich: \( x \in \mathbb{R} \setminus \{(2k+1)\frac{\pi}{2} | k \in \mathbb{Z}\} \)
- Wertebereich: \( y \in (-\infty, +\infty) \)
- Periodizität: \( \tan(x + \pi) = \tan(x) \)
- Symmetrie: Ungerade Funktion: \( \tan(-x) = -\tan(x) \)
- Spezielle Werte:
- \( \tan(0) = 0 \)
- \( \tan(45°) = \tan(\frac{\pi}{4}) = 1 \)
- \( \tan(60°) = \tan(\frac{\pi}{3}) = \sqrt{3} \approx 1.732 \)
- \( \tan(90°) = \tan(\frac{\pi}{2}) = \) nicht definiert
Praktische Anwendungen
- Vermessungswesen: Höhen- und Entfernungsberechnungen
- Bauingenieurwesen: Berechnung von Steigungen und Neigungen
- Navigation: Kursberechnungen und Richtungsbestimmung
- Physik: Berechnung von Geschwindigkeitsvektoren
- Architektur: Dachneigungen und Treppensteigungen
- Optik: Brechungswinkel und Lichtbrechung
- Maschinenbau: Berechnung von Winkeln bei Getrieben
Wichtiger Hinweis
Undefinierte Stellen: Der Tangens ist bei Winkeln von ±90°, ±270°, usw. (bzw. ±π/2, ±3π/2, ... in Radiant) nicht definiert, da an diesen Stellen der Kosinus gleich Null ist.
Periodizität: Die Tangens-Funktion wiederholt sich alle 180° (oder π Radiant). Dies bedeutet, dass tan(α) = tan(α + 180°).
Weitere wichtige Formeln
Additionstheorem:
\(\displaystyle \tan(a + b) = \frac{\tan(a) + \tan(b)}{1 - \tan(a)\tan(b)} \)
Doppelwinkelfunktion:
\(\displaystyle \tan(2\alpha) = \frac{2\tan(\alpha)}{1 - \tan^2(\alpha)} \)
|
|