Calculate Sigmoid Function
Online calculator and formulas for the Sigmoid function - The most important activation function in neural networks
Sigmoid Function Calculator
Sigmoid (Logistic) Function
The σ(x) or logistic function is the most important activation function in neural networks and Machine Learning.
S-shaped Sigmoid Curve
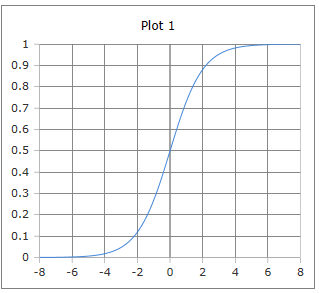
The logistic curve of the sigmoid function: S-shaped curve with values between 0 and 1.
Properties: Smoothly differentiable, monotonically increasing, symmetry around (0, 0.5).
|
|
What makes the Sigmoid function special?
The S-shaped curve of the Sigmoid function makes it ideal for many applications:
- Smooth transitions: No abrupt changes
- Bounded output: Always between 0 and 1
- Differentiability: Smoothly differentiable everywhere
- Probability interpretation: Perfect for binary classification
- Biological inspiration: Similar to neuron activation
- Mathematical elegance: Simple yet powerful formula
Sigmoid Function Formulas
Standard Form
Classic logistic function
Alternative Form
Equivalent exponential form
Tanh Representation
Hyperbolic tangent form
Derivative
Elegant derivative formula
Generalized Form
With parameters L, k, x₀
Logit Inversion
Sigmoid and logit are inverse
Properties
Special Values
Domain
All real numbers
Range
Always between 0 and 1
Application
Neural networks, Machine Learning, logistic regression, probability models.
Detailed Description of the Sigmoid Function
Mathematical Definition
The Sigmoid function, also known as the logistic function, is one of the most important S-shaped functions in mathematics. It maps reelle Zahlen to the interval (0,1) and is the foundation of many Machine Learning algorithms.
Using the Calculator
Enter any real number and click 'Calculate'. The function is defined for all reellen Zahlen and returns values between 0 and 1.
Historical Background
The logistic function was originally developed by Pierre François Verhulst in 1838 to describe population growth. In the 1940s, it was introduced by McCulloch and Pitts as an activation function for artificial neurons.
Properties and Applications
Machine Learning Applications
- Activation function in neural networks
- Binary classification (output layer)
- Logistic regression
- Gradient descent optimization
Scientific Applications
- Population dynamics (growth models)
- Epidemiology (spread models)
- Psychology (learning curves)
- Economics (adoption models)
Mathematical Properties
- Monotonicity: Strictly monotonically increasing
- Symmetry: σ(-x) = 1 - σ(x)
- Differentiability: Infinitely differentiable
- Limits: lim_{x→∞} σ(x) = 1, lim_{x→-∞} σ(x) = 0
Interesting Facts
- The derivative has the elegant form σ'(x) = σ(x)(1-σ(x))
- Maximum of the derivative at x = 0 with σ'(0) = 0.25
- Foundation of logistic regression and many deep learning models
- Can be limited by the vanishing gradient problem
Calculation Examples
Example 1
σ(0) = 0.5
Neutral input → 50% probability
Example 2
σ(2) ≈ 0.881
Positive input → High activation
Example 3
σ(-2) ≈ 0.119
Negative input → Low activation
Role in Neural Networks
Activation Function
In neural networks, the sigmoid function transforms the sum of weighted inputs:
Where wᵢ are the weights, xᵢ are the inputs, and b is the bias.
Backpropagation
The elegant derivative makes gradient calculation simple:
This enables efficient training through backpropagation.
Advantages and Disadvantages
Advantages
- Smooth, differentiable function
- Output between 0 and 1 (probability interpretation)
- Simple derivative
- Biologically plausible
Disadvantages
- Vanishing gradient problem in deep networks
- Not zero-centered (can slow convergence)
- Computationally intensive (exponential function)
- Saturation at large |x| values
|
|
|
|