Inverser hyperbolischer Kotangens

Berechnung des Winkels zum hyperbolischen Kotangens

ACoth Rechner

Diskontinuierliche Funktion

Die ACoth(x) oder inverse hyperbolische Kotangens zeigt diskontinuierliches Verhalten mit Polstelle bei x = ±1.

Eingabewert muss |x| > 1 sein (x < -1 oder x > 1)
Resultat
Winkel:

ACoth Funktionskurve

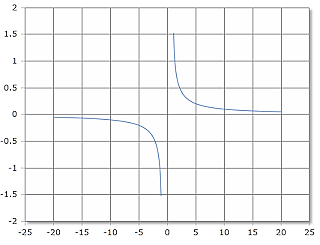
Kurve der ACoth Funktion

Die ACoth-Funktion hat Polstellen bei x = ±1 und ist diskontinuierlich.
Definitionsbereich: |x| > 1, Wertebereich: ℝ

Definitionsbereich der ACoth-Funktion

Die inverse hyperbolische Kotangens-Funktion hat einen kritischen Definitionsbereich:

  • Definitionsbereich: |x| > 1 (x < -1 oder x > 1)
  • Wertebereich: ℝ (alle reellen Zahlen)
  • Polstellen: x = ±1 (Singularitäten)
  • Verhalten: Zwei getrennte Äste
  • Asymptoten: Vertikale Asymptoten bei x = ±1
  • Ungültige Eingabe: -1 ≤ x ≤ 1 → undefiniert

Logarithmische Darstellung der ACoth-Funktion

Die inverse hyperbolische Kotangens-Funktion wird durch Logarithmus ausgedrückt:

Grundformel
\[\text{ACoth}(x) = \frac{1}{2} \ln \left( \frac{x + 1}{x - 1} \right)\]

Logarithmische Darstellung für |x| > 1

Umkehrrelation
\[\coth(\text{ACoth}(x)) = x\]

Für |x| > 1

Formeln zur ACoth-Funktion

Definition
\[\text{ACoth}(x) = \frac{1}{2} \ln \left( \frac{x + 1}{x - 1} \right)\]

Fundamentale logarithmische Darstellung für |x| > 1

Umkehrrelation
\[\coth(\text{ACoth}(x)) = x \quad \text{für } |x| > 1\]

Inverse Beziehung zum hyperbolischen Kotangens

Ableitung
\[\frac{d}{dx} \text{ACoth}(x) = \frac{1}{1-x^2}\]

Erste Ableitung für |x| > 1

Symmetrieeigenschaft
\[\text{ACoth}(-x) = -\text{ACoth}(x)\]

Ungerade Funktion (antisymmetrisch)

Grenzwertverhalten
\[\lim_{x \to 1^+} \text{ACoth}(x) = +\infty\] \[\lim_{x \to 1^-} \text{ACoth}(x) = -\infty\]

Verhalten an den Polstellen

Spezielle Werte

Wichtige Werte
ACoth(2) ≈ 0.549 ACoth(-2) ≈ -0.549 ACoth(3) ≈ 0.347
Polstellen
\[x = \pm 1: \text{ undefiniert}\]

Vertikale Asymptoten an diesen Stellen

Grenzwerte
\[\lim_{x \to \infty} \text{ACoth}(x) = 0\] \[\lim_{x \to -\infty} \text{ACoth}(x) = 0\]

Asymptotisches Verhalten gegen 0

Eigenschaften
  • Ungerade Funktion
  • Zwei getrennte Äste
  • Monoton fallend in jedem Ast
  • Horizontale Asymptote bei y = 0
Anwendungen

Hyperbolische Geometrie, Relativitätstheorie, spezielle Relativität, statistische Mechanik.

Ausführliche Beschreibung der ACoth-Funktion

Definition und Eingabe

Die inverse hyperbolische Kotangens-Funktion ACoth(x) ist die Umkehrfunktion des hyperbolischen Kotangens. Sie berechnet den Winkel, dessen hyperbolischer Kotangens dem gegebenen Wert entspricht.

Kritische Bedingung: Das Argument muss |x| > 1 sein!
Eingabebeschränkung

Das Argument muss kleiner als -1 oder größer als 1 sein. Werte im Intervall [-1, 1] sind nicht definiert, da der hyperbolische Kotangens in diesem Bereich nicht existiert.

Verwendung des Rechners

Geben Sie einen Wert mit |x| > 1 ein (x < -1 oder x > 1). Wählen Sie die gewünschte Maßeinheit (Grad oder Radiant) und die Anzahl der Dezimalstellen.

Resultat

Das Resultat wird in Grad (Vollkreis = 360°) oder Radiant (Vollkreis = 2π) angegeben. Die verwendete Maßeinheit wird mit dem entsprechenden Menü eingestellt.

Mathematische Eigenschaften

Funktionseigenschaften
  • Definitionsbereich: (-∞, -1) ∪ (1, ∞)
  • Wertebereich: ℝ (alle reellen Zahlen)
  • Polstellen: x = ±1 (vertikale Asymptoten)
  • Monotonie: Fallend in jedem Ast
Symmetrie und Verhalten
  • Ungerade Funktion: ACoth(-x) = -ACoth(x)
  • Horizontale Asymptote: y = 0 (für x → ±∞)
  • Zwei getrennte Äste bei x > 1 und x < -1
  • Stetig auf dem Definitionsbereich
Anwendungen
  • Hyperbolische Geometrie: Abstandsberechnungen
  • Relativitätstheorie: Geschwindigkeitstransformationen
  • Statistische Mechanik: Wahrscheinlichkeitsverteilungen
  • Integralrechnung: Partielle Bruchzerlegung
Praktische Hinweise
  • Zwei getrennte Funktionäste: positiver und negativer Bereich
  • Polstellen bei x = ±1: Funktion divergiert
  • Für |x| >> 1: ACoth(x) ≈ 1/x (Näherung)
  • Antisymmetrie nutzen: nur positiven Ast berechnen

Berechnungsbeispiele

Positive Werte

ACoth(2) ≈ 0.549

ACoth(3) ≈ 0.347

ACoth(10) ≈ 0.100

Negative Werte

ACoth(-2) ≈ -0.549

ACoth(-3) ≈ -0.347

ACoth(-10) ≈ -0.100

Grenzverhalten

x → 1⁺: ACoth(x) → +∞

x → 1⁻: ACoth(x) → -∞

x → ∞: ACoth(x) → 0


Informatik Funktionen

Dez-Hex-Bin-Oktal umwandeln • Bitweise schieben • Ein Bit setzen • Ein Bit zurücksetzen • Bitweise UND • Bitweise ODER • Bitweise exklusiv ODER

Spezial Funktionen

Airy • Abgeleitete Airy • Bessel I • Bessel Ie • Bessel J • Bessel Je • Bessel K • Bessel Ke • Bessel Y • Bessel Ye • Bessel Jv • Bessel Yv • Hankel • Beta • Unvollständige Beta • Inverse Unvollständige Beta • Binomialkoeffizient • Logarithmus des Binomialkoeffizienten • Erf • Erfc • Erfi • Erfci • Fibonacci • Fibonacci Tabelle • Gamma Funktion • Inverse Gamma • Log Gamma • Digamma • Trigamma • Logit • Sigmoid • Derivative Sigmoid • Softsign • Derivative Softsign • Softmax • Struve • Modifizierte Struve • Struve Tabelle • Modifizierte Struve Tabelle • Riemann Zeta

Hyperbolische Funktionen

ACosh • ACoth • ACsch • ASech • ASinh • ATanh • Cosh • Coth • Csch • Sech • Sinh • Tanh

Trigonometrische Funktionen

ACos • ACot • ACsc • ASec • ASin • ATan • Cos • Cot • Csc • Sec • Sin • Sinc • Tan • Grad in Radiant • Radiant in Grad