Inverse des hyperbolischen Kosekans

Berechnung des Winkels zum hyperbolischen Kosekans

ACsch Rechner

Inverse hyperbolische Funktion

Die ACsch(x) oder inverse hyperbolische Kosekans zeigt Polverhalten bei x = 0 und ist für alle x ≠ 0 definiert.

Eingabewert darf nicht 0 sein (x ≠ 0)
Resultat
Winkel:

ACsch Funktionskurve

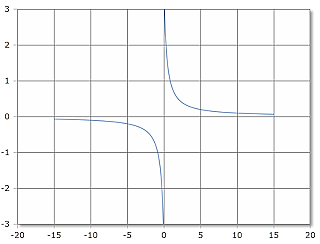
Kurve der ACsch Funktion

Die ACsch-Funktion hat eine Polstelle bei x = 0 und zwei separate Äste.
Definitionsbereich: x ≠ 0, Wertebereich: ℝ

Definitionsbereich der ACsch-Funktion

Die inverse hyperbolische Kosekans-Funktion hat einen einfachen Definitionsbereich:

  • Definitionsbereich: x ≠ 0 (alle reellen Zahlen außer 0)
  • Wertebereich: ℝ (alle reellen Zahlen)
  • Polstelle: x = 0 (Singularität)
  • Verhalten: Zwei getrennte Äste bei x > 0 und x < 0
  • Asymptote: Vertikale Asymptote bei x = 0
  • Bei x = 0: ACsch(0) → ∞ (unendlich)

Logarithmische Darstellung der ACsch-Funktion

Die inverse hyperbolische Kosekans-Funktion wird durch Logarithmus ausgedrückt:

Grundformel
\[\text{ACsch}(x) = \ln \left( \frac{1}{x} + \sqrt{\frac{1}{x^2} + 1} \right)\]

Logarithmische Darstellung für x ≠ 0

Umkehrrelation
\[\csch(\text{ACsch}(x)) = x\]

Für x ≠ 0

Formeln zur ACsch-Funktion

Definition
\[\text{ACsch}(x) = \ln \left( \frac{1}{x} + \sqrt{\frac{1}{x^2} + 1} \right)\]

Fundamentale logarithmische Darstellung für x ≠ 0

Umkehrrelation
\[\csch(\text{ACsch}(x)) = x \quad \text{für } x ≠ 0\]

Inverse Beziehung zum hyperbolischen Kosekans

Ableitung
\[\frac{d}{dx} \text{ACsch}(x) = -\frac{1}{|x|\sqrt{x^2+1}}\]

Erste Ableitung für x ≠ 0

Symmetrieeigenschaft
\[\text{ACsch}(-x) = -\text{ACsch}(x)\]

Ungerade Funktion (antisymmetrisch)

Grenzwertverhalten
\[\lim_{x \to 0^+} \text{ACsch}(x) = +\infty\] \[\lim_{x \to 0^-} \text{ACsch}(x) = -\infty\]

Verhalten an der Polstelle

Spezielle Werte

Wichtige Werte
ACsch(1) ≈ 0.881 ACsch(-1) ≈ -0.881 ACsch(2) ≈ 0.481
Polstelle
\[x = 0: \text{ undefiniert}\]

Vertikale Asymptote bei x = 0

Grenzwerte
\[\lim_{x \to \infty} \text{ACsch}(x) = 0\] \[\lim_{x \to -\infty} \text{ACsch}(x) = 0\]

Asymptotisches Verhalten gegen 0

Eigenschaften
  • Ungerade Funktion
  • Zwei getrennte Äste
  • Monoton fallend in jedem Ast
  • Horizontale Asymptote bei y = 0
Anwendungen

Hyperbolische Geometrie, Differentialgleichungen, Wellenphysik, statistische Mechanik.

Ausführliche Beschreibung der ACsch-Funktion

Definition und Eingabe

Die inverse hyperbolische Kosekans-Funktion ACsch(x) ist die Umkehrfunktion des hyperbolischen Kosekans. Sie berechnet den Winkel, dessen hyperbolischer Kosekans dem gegebenen Wert entspricht.

Definitionsbedingung: Das Argument muss x ≠ 0 sein!
Eingabebeschränkung

Das Argument kann eine positive oder negative Zahl sein, aber nicht 0. Bei x = 0 wird als Resultat ∞ (unendlich) zurückgegeben, da eine Polstelle vorliegt.

Verwendung des Rechners

Geben Sie einen beliebigen Wert ungleich 0 ein (x ≠ 0). Wählen Sie die gewünschte Maßeinheit (Grad oder Radiant) und die Anzahl der Dezimalstellen.

Resultat

Das Resultat wird in Grad (Vollkreis = 360°) oder Radiant (Vollkreis = 2π) angegeben. Die verwendete Maßeinheit wird mit dem entsprechenden Menü eingestellt.

Mathematische Eigenschaften

Funktionseigenschaften
  • Definitionsbereich: ℝ \ {0} (alle reellen Zahlen außer 0)
  • Wertebereich: ℝ (alle reellen Zahlen)
  • Polstelle: x = 0 (vertikale Asymptote)
  • Monotonie: Fallend in jedem Ast
Symmetrie und Verhalten
  • Ungerade Funktion: ACsch(-x) = -ACsch(x)
  • Horizontale Asymptote: y = 0 (für x → ±∞)
  • Zwei getrennte Äste bei x > 0 und x < 0
  • Stetig auf dem Definitionsbereich
Anwendungen
  • Hyperbolische Geometrie: Abstandsberechnungen
  • Differentialgleichungen: Lösungen spezieller DGL
  • Wellenphysik: Dispersionseigenschaften
  • Statistik: Spezielle Verteilungen
Praktische Hinweise
  • Zwei getrennte Funktionäste: positiver und negativer Bereich
  • Polstelle bei x = 0: Funktion divergiert
  • Für |x| >> 1: ACsch(x) ≈ ln(2/|x|) (Näherung)
  • Antisymmetrie nutzen: nur positiven Ast berechnen

Berechnungsbeispiele

Positive Werte

ACsch(1) ≈ 0.881

ACsch(2) ≈ 0.481

ACsch(0.5) ≈ 1.444

Negative Werte

ACsch(-1) ≈ -0.881

ACsch(-2) ≈ -0.481

ACsch(-0.5) ≈ -1.444

Grenzverhalten

x → 0⁺: ACsch(x) → +∞

x → 0⁻: ACsch(x) → -∞

x → ±∞: ACsch(x) → 0


Informatik Funktionen

Dez-Hex-Bin-Oktal umwandeln • Bitweise schieben • Ein Bit setzen • Ein Bit zurücksetzen • Bitweise UND • Bitweise ODER • Bitweise exklusiv ODER

Spezial Funktionen

Airy • Abgeleitete Airy • Bessel I • Bessel Ie • Bessel J • Bessel Je • Bessel K • Bessel Ke • Bessel Y • Bessel Ye • Bessel Jv • Bessel Yv • Hankel • Beta • Unvollständige Beta • Inverse Unvollständige Beta • Binomialkoeffizient • Logarithmus des Binomialkoeffizienten • Erf • Erfc • Erfi • Erfci • Fibonacci • Fibonacci Tabelle • Gamma Funktion • Inverse Gamma • Log Gamma • Digamma • Trigamma • Logit • Sigmoid • Derivative Sigmoid • Softsign • Derivative Softsign • Softmax • Struve • Modifizierte Struve • Struve Tabelle • Modifizierte Struve Tabelle • Riemann Zeta

Hyperbolische Funktionen

ACosh • ACoth • ACsch • ASech • ASinh • ATanh • Cosh • Coth • Csch • Sech • Sinh • Tanh

Trigonometrische Funktionen

ACos • ACot • ACsc • ASec • ASin • ATan • Cos • Cot • Csc • Sec • Sin • Sinc • Tan • Grad in Radiant • Radiant in Grad