Inverse des hyperbolischen Secans

Onlinerechner zur Berechnung des Winkels zum hyperbolischen Secans

ASech Rechner

Beschränkte Definitionsbereich

Die ASech(x) oder inverse hyperbolische Secans zeigt beschränktes Verhalten und ist nur für 0 < x ≤ 1 definiert.

Eingabewert muss zwischen 0 und 1 liegen (0 < x ≤ 1)
Resultat
Winkel:

ASech Funktionskurve

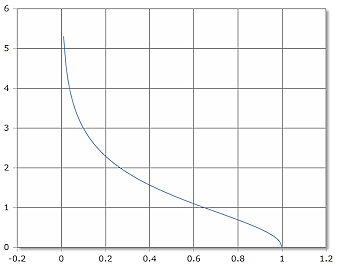
Kurve der ASech Funktion

Die ASech-Funktion ist nur für 0 < x ≤ 1 definiert und monoton fallend.
Definitionsbereich: (0, 1], Wertebereich: [0, ∞)

Beschränkter Definitionsbereich der ASech-Funktion

Die inverse hyperbolische Secans-Funktion hat einen sehr beschränkten Definitionsbereich:

  • Definitionsbereich: 0 < x ≤ 1
  • Wertebereich: [0, ∞)
  • Grenzverhalten: ASech(1) = 0
  • Monotonie: Streng monoton fallend
  • Asymptotik: ASech(x) → ∞ für x → 0⁺
  • Ungültige Eingabe: x ≤ 0 oder x > 1 → undefiniert

Logarithmische Darstellung der ASech-Funktion

Die inverse hyperbolische Secans-Funktion wird durch Logarithmus ausgedrückt:

Grundformel
\[\text{ASech}(x) = \ln \left( \frac{1 + \sqrt{1-x^2}}{x} \right)\]

Logarithmische Darstellung für 0 < x ≤ 1

Umkehrrelation
\[\sech(\text{ASech}(x)) = x\]

Für 0 < x ≤ 1

Formeln zur ASech-Funktion

Definition
\[\text{ASech}(x) = \ln \left( \frac{1 + \sqrt{1-x^2}}{x} \right)\]

Fundamentale logarithmische Darstellung für 0 < x ≤ 1

Umkehrrelation
\[\sech(\text{ASech}(x)) = x \quad \text{für } 0 < x ≤ 1\]

Inverse Beziehung zum hyperbolischen Secans

Ableitung
\[\frac{d}{dx} \text{ASech}(x) = -\frac{1}{x\sqrt{1-x^2}}\]

Erste Ableitung für 0 < x < 1

Alternative Darstellung
\[\text{ASech}(x) = \text{ACosh}\left(\frac{1}{x}\right)\]

Beziehung zur inversen hyperbolischen Kosinus-Funktion

Grenzwertverhalten
\[\lim_{x \to 1^-} \text{ASech}(x) = 0\] \[\lim_{x \to 0^+} \text{ASech}(x) = +\infty\]

Verhalten an den Definitionsbereichsgrenzen

Spezielle Werte

Wichtige Werte
ASech(1) = 0 ASech(0.5) ≈ 1.317 ASech(1/√2) ≈ 0.881
Grenzwerte
\[\lim_{x \to 1^-} \text{ASech}(x) = 0\] \[\lim_{x \to 0^+} \text{ASech}(x) = +\infty\]

Verhalten an den Definitionsbereichsgrenzen

Eigenschaften
  • Streng monoton fallend
  • Konkav (nach oben gekrümmt)
  • Beschränkter Definitionsbereich
  • Unbeschränkt wachsend bei x → 0⁺
Anwendungen

Hyperbolische Geometrie, Integralrechnung, spezielle Funktionen, Fourier-Analyse.

Ausführliche Beschreibung der ASech-Funktion

Definition und Eingabe

Die inverse hyperbolische Secans-Funktion ASech(x) ist die Umkehrfunktion des hyperbolischen Secans. Sie berechnet den Winkel, dessen hyperbolischer Secans dem gegebenen Wert entspricht.

Kritische Bedingung: Das Argument muss 0 < x ≤ 1 sein!
Eingabebeschränkung

Das Argument muss eine positive Zahl größer 0 und kleiner oder gleich 1 sein. Der hyperbolische Secans nimmt nur Werte in diesem Intervall an.

Verwendung des Rechners

Geben Sie einen Wert zwischen 0 und 1 ein (0 < x ≤ 1). Wählen Sie die gewünschte Maßeinheit (Grad oder Radiant) und die Anzahl der Dezimalstellen.

Resultat

Das Resultat wird in Grad (Vollkreis = 360°) oder Radiant (Vollkreis = 2π) angegeben. Die verwendete Maßeinheit wird mit dem entsprechenden Menü eingestellt.

Mathematische Eigenschaften

Funktionseigenschaften
  • Definitionsbereich: (0, 1]
  • Wertebereich: [0, ∞)
  • Randverhalten: ASech(1) = 0
  • Monotonie: Streng monoton fallend
Besondere Eigenschaften
  • Beschränkter Definitionsbereich
  • Unbeschränkter Wertebereich
  • Konvexe Funktion (nach oben gekrümmt)
  • Divergiert für x → 0⁺
Anwendungen
  • Hyperbolische Geometrie: Winkelmessungen
  • Integralrechnung: Spezielle Substitutionen
  • Fourier-Analysis: Transformationen
  • Differentialgleichungen: Spezielle Lösungen
Praktische Hinweise
  • ASech(1) = 0: Funktionswert am rechten Rand
  • Beziehung: ASech(x) = ACosh(1/x)
  • Für kleine x: ASech(x) ≈ ln(2/x) (Näherung)
  • Ableitung divergiert bei x = 1

Berechnungsbeispiele

Standardwerte

ASech(1) = 0

ASech(0.5) ≈ 1.317

ASech(1/e) ≈ 1.543

Spezielle Werte

ASech(1/√2) ≈ 0.881

ASech(0.1) ≈ 2.993

ASech(0.01) ≈ 4.605

Grenzverhalten

x → 1⁻: ASech(x) → 0

x → 0⁺: ASech(x) → +∞

Monoton fallend


Informatik Funktionen

Dez-Hex-Bin-Oktal umwandeln • Bitweise schieben • Ein Bit setzen • Ein Bit zurücksetzen • Bitweise UND • Bitweise ODER • Bitweise exklusiv ODER

Spezial Funktionen

Airy • Abgeleitete Airy • Bessel I • Bessel Ie • Bessel J • Bessel Je • Bessel K • Bessel Ke • Bessel Y • Bessel Ye • Bessel Jv • Bessel Yv • Hankel • Beta • Unvollständige Beta • Inverse Unvollständige Beta • Binomialkoeffizient • Logarithmus des Binomialkoeffizienten • Erf • Erfc • Erfi • Erfci • Fibonacci • Fibonacci Tabelle • Gamma Funktion • Inverse Gamma • Log Gamma • Digamma • Trigamma • Logit • Sigmoid • Derivative Sigmoid • Softsign • Derivative Softsign • Softmax • Struve • Modifizierte Struve • Struve Tabelle • Modifizierte Struve Tabelle • Riemann Zeta

Hyperbolische Funktionen

ACosh • ACoth • ACsch • ASech • ASinh • ATanh • Cosh • Coth • Csch • Sech • Sinh • Tanh

Trigonometrische Funktionen

ACos • ACot • ACsc • ASec • ASin • ATan • Cos • Cot • Csc • Sec • Sin • Sinc • Tan • Grad in Radiant • Radiant in Grad