Inverse des hyperbolischen Sinus

Berechnung des Winkels zum hyperbolischen Sinus

ASinh Rechner

Inverse hyperbolische Funktion

Die ASinh(x) oder inverse hyperbolische Sinus zeigt unbeschränktes Verhalten und ist für alle reellen Zahlen definiert.

Eingabewert kann eine beliebige positive oder negative Zahl sein
Resultat
Winkel:

ASinh Funktionskurve

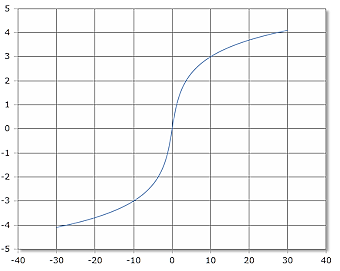
Kurve der ASinh Funktion

Die ASinh-Funktion ist für alle reellen Zahlen definiert und streng monoton steigend.
Definitionsbereich: ℝ, Wertebereich: ℝ

Unbeschränkter Definitionsbereich der ASinh-Funktion

Die inverse hyperbolische Sinus-Funktion hat den einfachsten Definitionsbereich aller inversen hyperbolischen Funktionen:

  • Definitionsbereich: ℝ (alle reellen Zahlen)
  • Wertebereich: ℝ (alle reellen Zahlen)
  • Nullstelle: ASinh(0) = 0
  • Monotonie: Streng monoton steigend
  • Symmetrie: Ungerade Funktion ASinh(-x) = -ASinh(x)
  • Stetigkeit: Überall stetig und differenzierbar

Logarithmische Darstellung der ASinh-Funktion

Die inverse hyperbolische Sinus-Funktion wird durch Logarithmus ausgedrückt:

Grundformel
\[\text{ASinh}(x) = \ln \left( x + \sqrt{x^2 + 1} \right)\]

Logarithmische Darstellung für alle x ∈ ℝ

Umkehrrelation
\[\sinh(\text{ASinh}(x)) = x\]

Für alle x ∈ ℝ

Formeln zur ASinh-Funktion

Definition
\[\text{ASinh}(x) = \ln \left( x + \sqrt{x^2 + 1} \right)\]

Fundamentale logarithmische Darstellung für alle x ∈ ℝ

Umkehrrelation
\[\sinh(\text{ASinh}(x)) = x \quad \text{für alle } x ∈ ℝ\]

Inverse Beziehung zum hyperbolischen Sinus

Ableitung
\[\frac{d}{dx} \text{ASinh}(x) = \frac{1}{\sqrt{x^2 + 1}}\]

Erste Ableitung für alle x ∈ ℝ

Symmetrieeigenschaft
\[\text{ASinh}(-x) = -\text{ASinh}(x)\]

Ungerade Funktion (antisymmetrisch)

Asymptotisches Verhalten
\[\text{ASinh}(x) \sim \ln(2|x|) + \text{sign}(x) \cdot \ln(2) \quad \text{für große } |x|\]

Näherung für sehr große Argumente

Spezielle Werte

Wichtige Werte
ASinh(0) = 0 ASinh(1) ≈ 0.881 ASinh(-1) ≈ -0.881
Nullstelle
\[\text{ASinh}(0) = 0\]

Eindeutige Nullstelle im Ursprung

Eigenschaften
  • Ungerade Funktion
  • Streng monoton steigend
  • Überall stetig und differenzierbar
  • Unbeschränkter Definitions- und Wertebereich
Verhalten
  • Wächst logarithmisch für große |x|
  • Approximiert ln(2|x|) für |x| >> 1
  • Linear für kleine |x| ≈ x
  • Wendepunkt im Ursprung
Anwendungen

Integralrechnung, hyperbolische Geometrie, Relativitätstheorie, Kettenlinien-Probleme.

Ausführliche Beschreibung der ASinh-Funktion

Definition und Eingabe

Die inverse hyperbolische Sinus-Funktion ASinh(x) ist die Umkehrfunktion des hyperbolischen Sinus. Sie berechnet den Winkel, dessen hyperbolischer Sinus dem gegebenen Wert entspricht.

Einfachste Definition: Das Argument kann jede reelle Zahl sein!
Eingabefreiheit

Das Argument kann eine positive oder negative Zahl sein. Die ASinh-Funktion ist als einzige der inversen hyperbolischen Funktionen für alle reellen Zahlen definiert.

Verwendung des Rechners

Geben Sie eine beliebige reelle Zahl ein. Es gibt keine Einschränkungen! Wählen Sie die gewünschte Maßeinheit (Grad oder Radiant) und die Anzahl der Dezimalstellen.

Resultat

Das Resultat wird in Grad (Vollkreis = 360°) oder Radiant (Vollkreis = 2π) angegeben. Die verwendete Maßeinheit wird mit dem entsprechenden Menü eingestellt.

Mathematische Eigenschaften

Funktionseigenschaften
  • Definitionsbereich: ℝ (alle reellen Zahlen)
  • Wertebereich: ℝ (alle reellen Zahlen)
  • Nullstelle: ASinh(0) = 0
  • Monotonie: Streng monoton steigend
Symmetrie und Verhalten
  • Ungerade Funktion: ASinh(-x) = -ASinh(x)
  • Keine Asymptoten oder Singularitäten
  • Überall stetig und differenzierbar
  • Konvex für x > 0, konkav für x < 0
Anwendungen
  • Integralrechnung: ∫ 1/√(x²+1) dx = ASinh(x)
  • Kettenlinien: Umkehrung von Sinus hyperbolicus
  • Relativitätstheorie: Rapidität-Transformationen
  • Hyperbolische Geometrie: Abstandsmessungen
Praktische Hinweise
  • Einfachste inverse hyperbolische Funktion
  • Keine Definitionsbereichseinschränkungen
  • Für große |x|: ASinh(x) ≈ ln(2|x|) + sign(x)·ln(2)
  • Für kleine |x|: ASinh(x) ≈ x (lineare Näherung)

Berechnungsbeispiele

Positive Werte

ASinh(1) ≈ 0.881

ASinh(2) ≈ 1.444

ASinh(10) ≈ 2.998

Negative Werte

ASinh(-1) ≈ -0.881

ASinh(-2) ≈ -1.444

ASinh(-10) ≈ -2.998

Spezielle Werte

ASinh(0) = 0

ASinh(e) ≈ 1.725

ASinh(100) ≈ 5.298

Integralverbindung

Stammfunktion
\[\int \frac{1}{\sqrt{x^2+1}} dx = \text{ASinh}(x) + C\]

Bedeutung: ASinh ist die Stammfunktion von 1/√(x²+1).

Praktische Anwendung
\[\int_0^a \frac{1}{\sqrt{x^2+1}} dx = \text{ASinh}(a)\]

Beispiel: Bogenlänge der Kettenlinie zwischen 0 und a.


Informatik Funktionen

Dez-Hex-Bin-Oktal umwandeln • Bitweise schieben • Ein Bit setzen • Ein Bit zurücksetzen • Bitweise UND • Bitweise ODER • Bitweise exklusiv ODER

Spezial Funktionen

Airy • Abgeleitete Airy • Bessel I • Bessel Ie • Bessel J • Bessel Je • Bessel K • Bessel Ke • Bessel Y • Bessel Ye • Bessel Jv • Bessel Yv • Hankel • Beta • Unvollständige Beta • Inverse Unvollständige Beta • Binomialkoeffizient • Logarithmus des Binomialkoeffizienten • Erf • Erfc • Erfi • Erfci • Fibonacci • Fibonacci Tabelle • Gamma Funktion • Inverse Gamma • Log Gamma • Digamma • Trigamma • Logit • Sigmoid • Derivative Sigmoid • Softsign • Derivative Softsign • Softmax • Struve • Modifizierte Struve • Struve Tabelle • Modifizierte Struve Tabelle • Riemann Zeta

Hyperbolische Funktionen

ACosh • ACoth • ACsch • ASech • ASinh • ATanh • Cosh • Coth • Csch • Sech • Sinh • Tanh

Trigonometrische Funktionen

ACos • ACot • ACsc • ASec • ASin • ATan • Cos • Cot • Csc • Sec • Sin • Sinc • Tan • Grad in Radiant • Radiant in Grad