Hyperbolischer Kosinus

Berechnung des hyperbolischen Kosinus eines Winkels

Cosh Rechner

Hyperbolische Funktion

Die Cosh(x) oder hyperbolische Kosinus zeigt Kettenlinie-Verhalten und ist für alle reellen Zahlen definiert.

Winkel kann eine beliebige reelle Zahl sein
Resultat
Cosh:

Cosh Funktionskurve

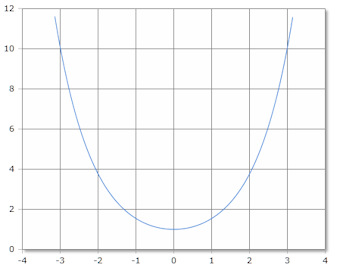
Kurve der Cosh Funktion

Die Cosh-Funktion ist eine gerade Funktion mit charakteristischer U-Form (Kettenlinie).
Definitionsbereich: ℝ, Wertebereich: [1, ∞)

Kettenlinie und natürliche Form der Cosh-Funktion

Die hyperbolische Kosinus-Funktion beschreibt die natürliche Form einer hängenden Kette:

  • Definitionsbereich: ℝ (alle reellen Zahlen)
  • Wertebereich: [1, ∞) (Minimum bei x = 0)
  • Minimum: Cosh(0) = 1
  • Symmetrie: Gerade Funktion Cosh(-x) = Cosh(x)
  • Monotonie: Fallend für x < 0, steigend für x > 0
  • Wachstum: Exponentielles Wachstum für große |x|

Exponentialfunktion-Darstellung der Cosh-Funktion

Die hyperbolische Kosinus-Funktion wird durch Exponentialfunktionen ausgedrückt:

Grundformel
\[\cosh(x) = \frac{e^x + e^{-x}}{2}\]

Exponentialfunktion-Darstellung für alle x ∈ ℝ

Umkehrrelation
\[\cosh(\text{ACosh}(x)) = x\]

Für x ≥ 1

Formeln zur Cosh-Funktion

Definition
\[\cosh(x) = \frac{e^x + e^{-x}}{2}\]

Fundamentale Exponentialfunktion-Darstellung für alle x ∈ ℝ

Identität mit Kosinus
\[\cosh(ix) = \cos(x)\]

Beziehung zum trigonometrischen Kosinus (Euler-Formel)

Ableitung
\[\frac{d}{dx} \cosh(x) = \sinh(x)\]

Erste Ableitung ist der hyperbolische Sinus

Additionstheorem
\[\cosh(x + y) = \cosh(x)\cosh(y) + \sinh(x)\sinh(y)\]

Hyperbolisches Additionstheorem

Hyperbolische Identität
\[\cosh^2(x) - \sinh^2(x) = 1\]

Fundamentale hyperbolische Identität (analog zu cos²+sin²=1)

Spezielle Werte

Wichtige Werte
Cosh(0) = 1 Cosh(1) ≈ 1.543 Cosh(ln(2)) = 1.25
Minimum
\[\min \cosh(x) = 1 \text{ bei } x = 0\]

Globales Minimum der Funktion

Eigenschaften
  • Gerade Funktion
  • Streng konvex
  • Überall stetig und differenzierbar
  • Exponentielles Wachstum für große |x|
Asymptotisches Verhalten
\[\cosh(x) \sim \frac{e^{|x|}}{2} \text{ für große } |x|\]

Exponentielles Wachstum

Anwendungen

Kettenlinie, Architektur (Bögen), Physik, Relativitätstheorie, Ingenieurwesen.

Ausführliche Beschreibung der Cosh-Funktion

Definition und Eingabe

Die hyperbolische Kosinus-Funktion Cosh(x) ist eine gerade und differenzierbare Funktion, die durch ihre Exponentialfunktion-Darstellung definiert ist.

Fundamentale Eigenschaft: Die Cosh-Funktion beschreibt die natürliche Form einer hängenden Kette!
Eingabe

Der Winkel wird in Grad (Vollkreis = 360°) oder Radiant (Vollkreis = 2π) angegeben. Die verwendete Maßeinheit wird mit dem Menü Grad oder Radiant eingestellt. Das Argument kann jede reelle Zahl sein.

Verwendung des Rechners

Geben Sie einen beliebigen Winkel ein. Es gibt keine Einschränkungen! Wählen Sie die gewünschte Maßeinheit (Grad oder Radiant) und die Anzahl der Dezimalstellen.

Resultat

Das Resultat ist immer ≥ 1, da die Cosh-Funktion ihr Minimum von 1 bei x = 0 hat. Die Funktion wächst exponentiell für große Beträge von x.

Mathematische Eigenschaften

Funktionseigenschaften
  • Definitionsbereich: ℝ (alle reellen Zahlen)
  • Wertebereich: [1, ∞)
  • Minimum: Cosh(0) = 1
  • Symmetrie: Gerade Funktion Cosh(-x) = Cosh(x)
Kettenlinie-Eigenschaften
  • Beschreibt die Form einer hängenden Kette
  • Optimale Form für gewölbte Brücken und Bögen
  • Minimiert die potentielle Energie
  • Gleichgewichtsform unter eigener Schwerkraft
Anwendungen
  • Architektur: Gewölbte Strukturen und Brücken
  • Physik: Relativistische Beziehungen
  • Ingenieurwesen: Kabelbrücken und Hängestrukturen
  • Mathematik: Hyperbolische Geometrie
Praktische Hinweise
  • Cosh(0) = 1: Minimum der Funktion
  • Gerade Funktion: Cosh(-x) = Cosh(x)
  • Exponentielles Wachstum: Cosh(x) ≈ e^|x|/2 für große |x|
  • Kettenlinie: y = a·cosh(x/a) für Parameter a

Berechnungsbeispiele

Grundwerte

Cosh(0) = 1

Cosh(1) ≈ 1.543

Cosh(-1) ≈ 1.543

Spezielle Werte

Cosh(ln(2)) = 1.25

Cosh(2) ≈ 3.762

Cosh(π) ≈ 11.592

Große Werte

Cosh(5) ≈ 74.210

Cosh(10) ≈ 11013.2

Exponentielles Wachstum

Kettenlinie-Anwendungen

Architektur und Bauingenieurwesen

Hängebrücken:

y = a·cosh(x/a) + h

Optimale Form für minimale Spannung

Beispiele: Gateway Arch (St. Louis), Gewölbebrücken, Kuppelstrukturen.

Physikalische Anwendungen

Hängende Kabel:

Gleichgewicht unter Schwerkraft

Minimale potentielle Energie

Anwendungen: Stromleitungen, Seile, flexible Strukturen.


Informatik Funktionen

Dez-Hex-Bin-Oktal umwandeln • Bitweise schieben • Ein Bit setzen • Ein Bit zurücksetzen • Bitweise UND • Bitweise ODER • Bitweise exklusiv ODER

Spezial Funktionen

Airy • Abgeleitete Airy • Bessel I • Bessel Ie • Bessel J • Bessel Je • Bessel K • Bessel Ke • Bessel Y • Bessel Ye • Bessel Jv • Bessel Yv • Hankel • Beta • Unvollständige Beta • Inverse Unvollständige Beta • Binomialkoeffizient • Logarithmus des Binomialkoeffizienten • Erf • Erfc • Erfi • Erfci • Fibonacci • Fibonacci Tabelle • Gamma Funktion • Inverse Gamma • Log Gamma • Digamma • Trigamma • Logit • Sigmoid • Derivative Sigmoid • Softsign • Derivative Softsign • Softmax • Struve • Modifizierte Struve • Struve Tabelle • Modifizierte Struve Tabelle • Riemann Zeta

Hyperbolische Funktionen

ACosh • ACoth • ACsch • ASech • ASinh • ATanh • Cosh • Coth • Csch • Sech • Sinh • Tanh

Trigonometrische Funktionen

ACos • ACot • ACsc • ASec • ASin • ATan • Cos • Cot • Csc • Sec • Sin • Sinc • Tan • Grad in Radiant • Radiant in Grad