Hyperbolischer Kosekans

Berechnung des hyperbolischen Kosekans eines Winkels

Csch Rechner

Polstelle bei x = 0

Die Csch(x) oder hyperbolische Kosekans zeigt Polverhalten mit einer Singularität bei x = 0.

Winkel darf nicht 0 sein (x ≠ 0)
Resultat
Csch:

Csch Funktionskurve

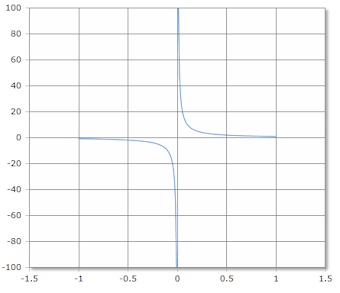
Kurve der Csch Funktion

Die Csch-Funktion hat eine Polstelle bei x = 0 und nähert sich asymptotisch 0.
Definitionsbereich: ℝ \ {0}, Wertebereich: ℝ \ {0}

Polstelle und asymptotisches Verhalten der Csch-Funktion

Die hyperbolische Kosekans-Funktion zeigt charakteristische Singularität:

  • Definitionsbereich: ℝ \ {0} (alle reellen Zahlen außer 0)
  • Wertebereich: ℝ \ {0} (alle reellen Zahlen außer 0)
  • Polstelle: x = 0 (Singularität)
  • Asymptoten: Horizontale Asymptote bei y = 0
  • Symmetrie: Ungerade Funktion Csch(-x) = -Csch(x)
  • Monotonie: Streng monoton fallend in jedem Ast

Exponentialfunktion-Darstellung der Csch-Funktion

Die hyperbolische Kosekans-Funktion wird durch Exponentialfunktionen ausgedrückt:

Grundformel
\[\csch(x) = \frac{1}{\sinh(x)} = \frac{2}{e^x - e^{-x}}\]

Kehrwert des hyperbolischen Sinus für x ≠ 0

Umkehrrelation
\[\sinh(x) \cdot \csch(x) = 1\]

Für x ≠ 0

Formeln zur Csch-Funktion

Definition als Kehrwert
\[\csch(x) = \frac{1}{\sinh(x)}\]

Kehrwert des hyperbolischen Sinus

Exponentialform
\[\csch(x) = \frac{2}{e^x - e^{-x}}\]

Direkte Exponentialfunktion-Darstellung für x ≠ 0

Ableitung
\[\frac{d}{dx} \csch(x) = -\csch(x) \coth(x) = -\frac{\coth(x)}{\sinh(x)}\]

Erste Ableitung für x ≠ 0

Symmetrieeigenschaft
\[\csch(-x) = -\csch(x)\]

Ungerade Funktion (antisymmetrisch)

Grenzwertverhalten
\[\lim_{x \to 0^+} \csch(x) = +\infty\] \[\lim_{x \to 0^-} \csch(x) = -\infty\] \[\lim_{x \to \pm\infty} \csch(x) = 0\]

Verhalten an Polstelle und asymptotisch

Spezielle Werte

Wichtige Werte
Csch(1) ≈ 0.851 Csch(-1) ≈ -0.851 Csch(2) ≈ 0.276
Polstelle
\[x = 0: \text{ undefiniert}\]

Vertikale Asymptote bei x = 0

Asymptote
\[y = 0 \text{ für } x \to \pm\infty\]

Horizontale Asymptote

Eigenschaften
  • Ungerade Funktion
  • Streng monoton fallend in jedem Ast
  • Zwei getrennte Äste
  • Horizontale Asymptote bei y = 0
Verhalten
  • Exponentiell fallend für große |x|
  • Approximiert 2e^(-|x|) für |x| >> 1
  • Divergiert bei x → 0
  • Kehrwert des Sinh
Anwendungen

Wellenphysik, Feldtheorie, hyperbolische Geometrie, spezielle Relativitätstheorie.

Ausführliche Beschreibung der Csch-Funktion

Definition und Eingabe

Die hyperbolische Kosekans-Funktion Csch(x) ist der Kehrwert des hyperbolischen Sinus. Sie gehört zur Familie der hyperbolischen Funktionen und zeigt charakteristisches Polverhalten bei x = 0.

Kritische Eigenschaft: Die Csch-Funktion hat eine Polstelle bei x = 0!
Eingabe

Der Winkel wird in Grad (Vollkreis = 360°) oder Radiant (Vollkreis = 2π) angegeben. Die verwendete Maßeinheit wird mit dem Menü Grad oder Radiant eingestellt. Wichtig: Der Winkel darf nicht 0 sein!

Verwendung des Rechners

Geben Sie einen Winkel ungleich 0 ein. Bei x = 0 ist die Funktion nicht definiert! Wählen Sie die gewünschte Maßeinheit (Grad oder Radiant) und die Anzahl der Dezimalstellen.

Resultat

Das Resultat kann sowohl positive als auch negative Werte annehmen. Für große |x| nähert sich Csch(x) exponentiell der 0. Die Funktion zeigt zwei getrennte Äste für positive und negative x-Werte.

Mathematische Eigenschaften

Funktionseigenschaften
  • Definitionsbereich: ℝ \ {0} (alle reellen Zahlen außer 0)
  • Wertebereich: ℝ \ {0} (alle reellen Zahlen außer 0)
  • Polstelle: x = 0 (vertikale Asymptote)
  • Symmetrie: Ungerade Funktion Csch(-x) = -Csch(x)
Asymptotisches Verhalten
  • Horizontale Asymptote bei y = 0
  • Vertikale Asymptote bei x = 0
  • Streng monoton fallend in jedem Ast
  • Exponentiell fallend für große |x|
Anwendungen
  • Wellenphysik: Wellenausbreitung und Dämpfung
  • Feldtheorie: Elektromagnetische Felder
  • Relativitätstheorie: Lorentz-Transformationen
  • Hyperbolische Geometrie: Abstandsmessungen
Praktische Hinweise
  • Polstelle bei x = 0: Funktion divergiert
  • Ungerade Funktion: Csch(-x) = -Csch(x)
  • Kehrwert: Csch(x) = 1/Sinh(x)
  • Für große |x|: Csch(x) ≈ 2e^(-|x|)

Berechnungsbeispiele

Positive Werte

Csch(1) ≈ 0.851

Csch(2) ≈ 0.276

Csch(5) ≈ 0.013

Negative Werte

Csch(-1) ≈ -0.851

Csch(-2) ≈ -0.276

Csch(-5) ≈ -0.013

Grenzverhalten

x → 0⁺: Csch(x) → +∞

x → 0⁻: Csch(x) → -∞

x → ±∞: Csch(x) → 0

Physikalische Anwendungen

Wellenphysik und Dämpfung

Gedämpfte Schwingungen:

A(t) = A₀ · csch(γt)

Amplitudenverhalten

Anwendung: Exponentiell gedämpfte Wellensysteme.

Elektromagnetische Felder

Feldverteilungen:

E(r) ∝ csch(kr)

Abschirmungseffekte

Beispiel: Felder in leitenden Medien.

Wichtige mathematische Beziehungen

Beziehung zu anderen hyperbolischen Funktionen
\[\csch(x) = \frac{1}{\sinh(x)}\] \[\csch^2(x) = \coth^2(x) - 1\]

Identitäten: Fundamentale hyperbolische Beziehungen.

Asymptotische Entwicklung
\[\csch(x) \approx \frac{2}{e^{|x|}} \text{ für große } |x|\] \[\csch(x) \approx \frac{1}{x} \text{ für kleine } |x|\]

Näherungen: Verhalten in verschiedenen Bereichen.


Informatik Funktionen

Dez-Hex-Bin-Oktal umwandeln • Bitweise schieben • Ein Bit setzen • Ein Bit zurücksetzen • Bitweise UND • Bitweise ODER • Bitweise exklusiv ODER

Spezial Funktionen

Airy • Abgeleitete Airy • Bessel I • Bessel Ie • Bessel J • Bessel Je • Bessel K • Bessel Ke • Bessel Y • Bessel Ye • Bessel Jv • Bessel Yv • Hankel • Beta • Unvollständige Beta • Inverse Unvollständige Beta • Binomialkoeffizient • Logarithmus des Binomialkoeffizienten • Erf • Erfc • Erfi • Erfci • Fibonacci • Fibonacci Tabelle • Gamma Funktion • Inverse Gamma • Log Gamma • Digamma • Trigamma • Logit • Sigmoid • Derivative Sigmoid • Softsign • Derivative Softsign • Softmax • Struve • Modifizierte Struve • Struve Tabelle • Modifizierte Struve Tabelle • Riemann Zeta

Hyperbolische Funktionen

ACosh • ACoth • ACsch • ASech • ASinh • ATanh • Cosh • Coth • Csch • Sech • Sinh • Tanh

Trigonometrische Funktionen

ACos • ACot • ACsc • ASec • ASin • ATan • Cos • Cot • Csc • Sec • Sin • Sinc • Tan • Grad in Radiant • Radiant in Grad