Hyperbolischer Sekans

Berechnung des hyperbolischen Sekans eines Winkels

Sech Rechner

Glockenförmige Funktion

Die Sech(x) oder hyperbolische Sekans zeigt glockenförmiges Verhalten und ist der Kehrwert von Cosh(x).

Winkel kann eine beliebige reelle Zahl sein
Resultat
Sech:

Sech Funktionskurve

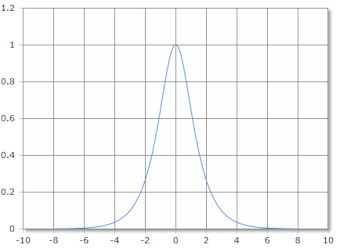
Kurve der Sech Funktion

Die Sech-Funktion ist glockenförmig mit Maximum bei x = 0 und nähert sich asymptotisch 0.
Definitionsbereich: ℝ, Wertebereich: (0, 1]

Glockenförmiges Verhalten der Sech-Funktion

Die hyperbolische Sekans-Funktion zeigt charakteristische Glockenkurven-Eigenschaften:

  • Definitionsbereich: ℝ (alle reellen Zahlen)
  • Wertebereich: (0, 1] (positive Werte bis 1)
  • Maximum: Sech(0) = 1
  • Symmetrie: Gerade Funktion Sech(-x) = Sech(x)
  • Monotonie: Fallend für |x| > 0
  • Asymptoten: Horizontale Asymptote bei y = 0

Exponentialfunktion-Darstellung der Sech-Funktion

Die hyperbolische Sekans-Funktion wird durch Exponentialfunktionen ausgedrückt:

Grundformel
\[\sech(x) = \frac{1}{\cosh(x)} = \frac{2}{e^x + e^{-x}}\]

Kehrwert des hyperbolischen Kosinus für alle x ∈ ℝ

Umkehrrelation
\[\cosh(x) \cdot \sech(x) = 1\]

Für alle x ∈ ℝ

Formeln zur Sech-Funktion

Definition als Kehrwert
\[\sech(x) = \frac{1}{\cosh(x)}\]

Kehrwert des hyperbolischen Kosinus

Exponentialform
\[\sech(x) = \frac{2}{e^x + e^{-x}}\]

Direkte Exponentialfunktion-Darstellung für alle x ∈ ℝ

Ableitung
\[\frac{d}{dx} \sech(x) = -\sech(x) \tanh(x) = -\frac{\tanh(x)}{\cosh(x)}\]

Erste Ableitung für alle x ∈ ℝ

Symmetrieeigenschaft
\[\sech(-x) = \sech(x)\]

Gerade Funktion (symmetrisch)

Grenzwertverhalten
\[\lim_{x \to \pm\infty} \sech(x) = 0\] \[\max \sech(x) = \sech(0) = 1\]

Asymptotisches Verhalten und Maximum

Spezielle Werte

Wichtige Werte
Sech(0) = 1 Sech(1) ≈ 0.648 Sech(2) ≈ 0.266
Maximum
\[\max \sech(x) = 1 \text{ bei } x = 0\]

Globales Maximum der Funktion

Eigenschaften
  • Gerade Funktion
  • Glockenförmige Kurve
  • Überall stetig und differenzierbar
  • Exponentiell fallend für große |x|
Asymptotisches Verhalten
\[\sech(x) \sim 2e^{-|x|} \text{ für große } |x|\]

Exponentieller Abfall

Anwendungen

Soliton-Theorie, nichtlineare Optik, Wellengleichungen, Quantenmechanik.

Ausführliche Beschreibung der Sech-Funktion

Definition und Eingabe

Die hyperbolische Sekans-Funktion Sech(x) ist der Kehrwert des hyperbolischen Kosinus. Sie gehört zur Familie der hyperbolischen Funktionen und zeigt eine charakteristische glockenförmige Kurve.

Charakteristische Eigenschaft: Die Sech-Funktion hat eine perfekte Glockenkurven-Form!
Eingabe

Der Winkel wird in Grad (Vollkreis = 360°) oder Radiant (Vollkreis = 2π) angegeben. Die verwendete Maßeinheit wird mit dem Menü Grad oder Radiant eingestellt. Das Argument kann jede reelle Zahl sein.

Verwendung des Rechners

Geben Sie einen beliebigen Winkel ein. Es gibt keine Einschränkungen! Wählen Sie die gewünschte Maßeinheit (Grad oder Radiant) und die Anzahl der Dezimalstellen.

Resultat

Das Resultat liegt immer zwischen 0 und 1, wobei das Maximum von 1 bei x = 0 erreicht wird. Die Funktion fällt exponentiell ab, wenn |x| zunimmt, und nähert sich asymptotisch der 0.

Mathematische Eigenschaften

Funktionseigenschaften
  • Definitionsbereich: ℝ (alle reellen Zahlen)
  • Wertebereich: (0, 1] (positive Werte bis 1)
  • Maximum: Sech(0) = 1
  • Symmetrie: Gerade Funktion Sech(-x) = Sech(x)
Glockenförmige Eigenschaften
  • Perfekte Glockenkurven-Form
  • Symmetrisch um die y-Achse
  • Exponentiell fallende Flanken
  • Eindeutiges Maximum bei x = 0
Anwendungen
  • Soliton-Theorie: Sech²-Pulse in nichtlinearen Medien
  • Nichtlineare Optik: Optische Solitonen
  • Quantenmechanik: Wellenfunktionen gebundener Zustände
  • Signalverarbeitung: Glockenkurven-Filter
Praktische Hinweise
  • Gerade Funktion: Sech(-x) = Sech(x)
  • Kehrwert: Sech(x) = 1/Cosh(x)
  • Für große |x|: Sech(x) ≈ 2e^(-|x|)
  • Soliton-Lösung: Sech²(x) in KdV-Gleichung

Berechnungsbeispiele

Grundwerte

Sech(0) = 1

Sech(1) ≈ 0.648

Sech(-1) ≈ 0.648

Mittlere Werte

Sech(2) ≈ 0.266

Sech(π) ≈ 0.086

Sech(3) ≈ 0.099

Große Werte

Sech(5) ≈ 0.013

Sech(10) ≈ 0.00009

x → ±∞: Sech(x) → 0

Soliton-Anwendungen

Optische Solitonen

Sech²-Pulse:

u(x,t) = A·sech²((x-vt)/w)

Selbsterhaltende Wellenformen

Anwendung: Glasfaser-Kommunikation, nichtlineare Optik.

Quantenmechanik

Pöschl-Teller-Potential:

ψ(x) ∝ sech^n(αx)

Gebundene Zustände

Beispiel: Exakt lösbare Wellenfunktionen.

Wichtige mathematische Beziehungen

Beziehung zu anderen hyperbolischen Funktionen
\[\sech(x) = \frac{1}{\cosh(x)}\] \[1 - \tanh^2(x) = \sech^2(x)\]

Identitäten: Fundamentale hyperbolische Beziehungen.

Integrale und Ableitungen
\[\int \sech(x) dx = \arctan(\sinh(x))\] \[\frac{d}{dx}\sech(x) = -\sech(x)\tanh(x)\]

Stammfunktion: Arkustangens des hyperbolischen Sinus.


Informatik Funktionen

Dez-Hex-Bin-Oktal umwandeln • Bitweise schieben • Ein Bit setzen • Ein Bit zurücksetzen • Bitweise UND • Bitweise ODER • Bitweise exklusiv ODER

Spezial Funktionen

Airy • Abgeleitete Airy • Bessel I • Bessel Ie • Bessel J • Bessel Je • Bessel K • Bessel Ke • Bessel Y • Bessel Ye • Bessel Jv • Bessel Yv • Hankel • Beta • Unvollständige Beta • Inverse Unvollständige Beta • Binomialkoeffizient • Logarithmus des Binomialkoeffizienten • Erf • Erfc • Erfi • Erfci • Fibonacci • Fibonacci Tabelle • Gamma Funktion • Inverse Gamma • Log Gamma • Digamma • Trigamma • Logit • Sigmoid • Derivative Sigmoid • Softsign • Derivative Softsign • Softmax • Struve • Modifizierte Struve • Struve Tabelle • Modifizierte Struve Tabelle • Riemann Zeta

Hyperbolische Funktionen

ACosh • ACoth • ACsch • ASech • ASinh • ATanh • Cosh • Coth • Csch • Sech • Sinh • Tanh

Trigonometrische Funktionen

ACos • ACot • ACsc • ASec • ASin • ATan • Cos • Cot • Csc • Sec • Sin • Sinc • Tan • Grad in Radiant • Radiant in Grad