Hyperbolic Tangent

Calculator and formula for calculating the hyperbolic tangent of an angle

Tanh Calculator

Sigmoid Function

The Tanh(x) or hyperbolic tangent shows sigmoid behavior with range [-1, 1].

Angle can be any real number
Results
Tanh:
Complex Numbers

You can find the Tanh function for calculating a complex number here

Tanh Function Curve

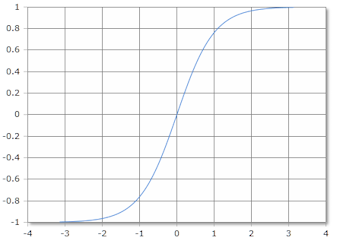
Curve of the Tanh function

The Tanh function is S-shaped with horizontal asymptotes at y = ±1.
Domain: ℝ, Range: (-1, 1)
Unit of measurement for the X axis is radians

Sigmoid Behavior of the Tanh Function

The hyperbolic tangent function exhibits characteristic sigmoid properties:

  • Domain: ℝ (all real numbers)
  • Range: (-1, 1) (bounded between -1 and 1)
  • Zero: Tanh(0) = 0
  • Symmetry: Odd function Tanh(-x) = -Tanh(x)
  • Asymptotes: Horizontal at y = ±1
  • Monotonicity: Strictly monotonically increasing

Exponential Function Representation of the Tanh Function

The hyperbolic tangent function is expressed through exponential functions:

Basic Formula
\[\tanh(x) = \frac{\sinh(x)}{\cosh(x)} = \frac{e^x - e^{-x}}{e^x + e^{-x}}\]

Ratio of Sinh to Cosh for all x ∈ ℝ

Alternative Form
\[\tanh(x) = \frac{e^{2x} - 1}{e^{2x} + 1}\]

Simplified exponential form

Formulas for the Tanh Function

Definition as Ratio
\[\tanh(x) = \frac{\sinh(x)}{\cosh(x)}\]

Ratio of hyperbolic sine to hyperbolic cosine

Exponential Forms
\[\tanh(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}} = \frac{e^{2x} - 1}{e^{2x} + 1}\]

Various exponential function representations

Derivative
\[\frac{d}{dx} \tanh(x) = \text{sech}^2(x) = 1 - \tanh^2(x)\]

First derivative for all x ∈ ℝ

Symmetry Property
\[\tanh(-x) = -\tanh(x)\]

Odd function (antisymmetric)

Limit Behavior
\[\lim_{x \to +\infty} \tanh(x) = +1\] \[\lim_{x \to -\infty} \tanh(x) = -1\]

Horizontal asymptotes at y = ±1

Special Values

Important Values
Tanh(0) = 0 Tanh(1) ≈ 0.762 Tanh(∞) = 1
Range
\[-1 < \tanh(x) < 1\]

Bounded output between -1 and +1

Properties
  • Odd function
  • Strictly monotonically increasing
  • Sigmoid S-curve
  • Bounded range
Asymptotic Behavior
\[\tanh(x) \approx 1 - 2e^{-2x} \text{ for large } x\]

Exponential approach to ±1

Applications

Neural networks, machine learning, activation functions, signal processing.

Detailed Description of the Tanh Function

Definition and Input

The hyperbolic tangent function Tanh(x) is a mathematical function from the family of hyperbolic functions. It exhibits characteristic sigmoid behavior with a bounded range.

Characteristic Property: The Tanh function is bounded to the interval (-1, 1)!
Input

The angle is given in degrees (full circle = 360°) or radians (full circle = 2π). The unit of measurement used is set using the Degrees or Radians menu. The argument can be any real number.

Output

The range of the result is -1 to +1. The function approaches these limit values asymptotically but never reaches them exactly for finite input values.

Using the Calculator

Enter any angle. The Tanh function is defined for all real numbers and always returns a value between -1 and 1.

Mathematical Properties

Function Properties
  • Domain: ℝ (all real numbers)
  • Range: (-1, 1) (bounded)
  • Zero: Tanh(0) = 0
  • Symmetry: Odd function Tanh(-x) = -Tanh(x)
Sigmoid Properties
  • S-shaped curve through the origin
  • Horizontal asymptotes at y = ±1
  • Steep rise around x = 0
  • Smooth transition between extreme values
Applications
  • Neural Networks: Activation function
  • Machine Learning: Sigmoid normalization
  • Signal Processing: Nonlinear transformation
  • Control Engineering: Saturation functions
Practical Notes
  • Tanh(0) = 0: Symmetry center of the function
  • Bounded: -1 < Tanh(x) < 1 for all x
  • For large |x|: Tanh(x) ≈ ±1 · (1 - 2e^(-2|x|))
  • For small |x|: Tanh(x) ≈ x (linear approximation)

Calculation Examples

Small Values

Tanh(0) = 0

Tanh(0.5) ≈ 0.462

Tanh(1) ≈ 0.762

Medium Values

Tanh(2) ≈ 0.964

Tanh(3) ≈ 0.995

Tanh(-2) ≈ -0.964

Limits

x → +∞: Tanh(x) → 1

x → -∞: Tanh(x) → -1

Never exactly ±1

Applications in Artificial Intelligence

Neural Networks

Activation Function:

y = tanh(wx + b)

Nonlinear transformation

Advantage: Symmetric around 0, steep gradient transitions.

Signal Processing

Saturation Function:

Limits output signals

Prevents overdrive

Application: Adaptive filters, control systems.

Important Mathematical Relationships

Relationship to Other Hyperbolic Functions
\[\tanh(x) = \frac{\sinh(x)}{\cosh(x)}\] \[\text{sech}^2(x) = 1 - \tanh^2(x)\]

Identities: Fundamental hyperbolic relationships.

Integrals and Series
\[\int \tanh(x) dx = \ln(\cosh(x)) + C\] \[\tanh(x) = \sum_{n=1}^{\infty} \frac{B_{2n} 2^{2n} (2^{2n}-1)}{(2n)!} x^{2n-1}\]

Antiderivative: Natural logarithm of Cosh.


IT Functions

Decimal, Hex, Bin, Octal conversion • Shift bits left or right • Set a bit • Clear a bit • Bitwise AND • Bitwise OR • Bitwise exclusive OR

Special functions

Airy • Derivative Airy • Bessel-I • Bessel-Ie • Bessel-J • Bessel-Je • Bessel-K • Bessel-Ke • Bessel-Y • Bessel-Ye • Spherical-Bessel-J • Spherical-Bessel-Y • Hankel • Beta • Incomplete Beta • Incomplete Inverse Beta • Binomial Coefficient • Binomial Coefficient Logarithm • Erf • Erfc • Erfi • Erfci • Fibonacci • Fibonacci Tabelle • Gamma • Inverse Gamma • Log Gamma • Digamma • Trigamma • Logit • Sigmoid • Derivative Sigmoid • Softsign • Derivative Softsign • Softmax • Struve • Struve table • Modified Struve • Modified Struve table • Riemann Zeta

Hyperbolic functions

ACosh • ACoth • ACsch • ASech • ASinh • ATanh • Cosh • Coth • Csch • Sech • Sinh • Tanh

Trigonometrische Funktionen

ACos • ACot • ACsc • ASec • ASin • ATan • Cos • Cot • Csc • Sec • Sin • Sinc • Tan • Degree to Radian • Radian to Degree