Hyperbolischer Tangens

Rechner und Formel zur Berechnung des hyperbolischen Tangens eines Winkels

Tanh Rechner

Sigmoidfunktion

Die Tanh(x) oder hyperbolische Tangens zeigt sigmoidales Verhalten mit Wertebereich [-1, 1].

Winkel kann eine beliebige reelle Zahl sein
Resultat
Tanh:

Tanh Funktionskurve

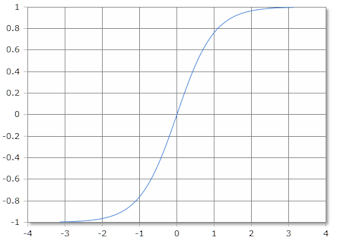
Kurve der Tanh Funktion

Die Tanh-Funktion ist S-förmig mit horizontalen Asymptoten bei y = ±1.
Definitionsbereich: ℝ, Wertebereich: (-1, 1)
Maßeinheit der X-Achse ist Radiant

Sigmoidales Verhalten der Tanh-Funktion

Die hyperbolische Tangens-Funktion zeigt charakteristische Sigmoid-Eigenschaften:

  • Definitionsbereich: ℝ (alle reellen Zahlen)
  • Wertebereich: (-1, 1) (beschränkt zwischen -1 und 1)
  • Nullstelle: Tanh(0) = 0
  • Symmetrie: Ungerade Funktion Tanh(-x) = -Tanh(x)
  • Asymptoten: Horizontal bei y = ±1
  • Monotonie: Streng monoton steigend

Exponentialfunktion-Darstellung der Tanh-Funktion

Die hyperbolische Tangens-Funktion wird durch Exponentialfunktionen ausgedrückt:

Grundformel
\[\tanh(x) = \frac{\sinh(x)}{\cosh(x)} = \frac{e^x - e^{-x}}{e^x + e^{-x}}\]

Verhältnis von Sinh zu Cosh für alle x ∈ ℝ

Alternative Form
\[\tanh(x) = \frac{e^{2x} - 1}{e^{2x} + 1}\]

Vereinfachte Exponentialform

Formeln zur Tanh-Funktion

Definition als Verhältnis
\[\tanh(x) = \frac{\sinh(x)}{\cosh(x)}\]

Verhältnis von hyperbolischem Sinus zu hyperbolischem Kosinus

Exponentialformen
\[\tanh(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}} = \frac{e^{2x} - 1}{e^{2x} + 1}\]

Verschiedene Exponentialfunktion-Darstellungen

Ableitung
\[\frac{d}{dx} \tanh(x) = \sech^2(x) = 1 - \tanh^2(x)\]

Erste Ableitung für alle x ∈ ℝ

Symmetrieeigenschaft
\[\tanh(-x) = -\tanh(x)\]

Ungerade Funktion (antisymmetrisch)

Grenzwertverhalten
\[\lim_{x \to +\infty} \tanh(x) = +1\] \[\lim_{x \to -\infty} \tanh(x) = -1\]

Horizontale Asymptoten bei y = ±1

Spezielle Werte

Wichtige Werte
Tanh(0) = 0 Tanh(1) ≈ 0.762 Tanh(∞) = 1
Wertebereich
\[-1 < \tanh(x) < 1\]

Beschränkte Ausgabe zwischen -1 und +1

Eigenschaften
  • Ungerade Funktion
  • Streng monoton steigend
  • Sigmoidale S-Kurve
  • Beschränkter Wertebereich
Asymptotisches Verhalten
\[\tanh(x) \approx 1 - 2e^{-2x} \text{ für große } x\]

Exponentieller Ansatz an ±1

Anwendungen

Neuronale Netze, maschinelles Lernen, Aktivierungsfunktionen, Signalverarbeitung.

Ausführliche Beschreibung der Tanh-Funktion

Definition und Eingabe

Die hyperbolische Tangens-Funktion Tanh(x) ist eine mathematische Funktion aus der Familie der Hyperbelfunktionen. Sie zeigt charakteristisches sigmoidales Verhalten mit beschränktem Wertebereich.

Charakteristische Eigenschaft: Die Tanh-Funktion ist auf das Intervall (-1, 1) beschränkt!
Eingabe

Der Winkel wird in Grad (Vollkreis = 360°) oder Radiant (Vollkreis = 2π) angegeben. Die verwendete Maßeinheit wird mit dem Menü Grad oder Radiant eingestellt. Das Argument kann jede reelle Zahl sein.

Ausgabe

Der Bereich des Resultats ist -1 bis +1. Die Funktion erreicht diese Grenzwerte asymptotisch, erreicht sie aber nie exakt für endliche Eingabewerte.

Verwendung des Rechners

Geben Sie einen beliebigen Winkel ein. Die Tanh-Funktion ist für alle reellen Zahlen definiert und liefert immer einen Wert zwischen -1 und 1.

Mathematische Eigenschaften

Funktionseigenschaften
  • Definitionsbereich: ℝ (alle reellen Zahlen)
  • Wertebereich: (-1, 1) (beschränkt)
  • Nullstelle: Tanh(0) = 0
  • Symmetrie: Ungerade Funktion Tanh(-x) = -Tanh(x)
Sigmoid-Eigenschaften
  • S-förmige Kurve durch den Ursprung
  • Horizontale Asymptoten bei y = ±1
  • Steiler Anstieg um x = 0
  • Glatter Übergang zwischen Extremwerten
Anwendungen
  • Neuronale Netze: Aktivierungsfunktion
  • Maschinelles Lernen: Sigmoid-Normalisierung
  • Signalverarbeitung: Nichtlineare Transformation
  • Regelungstechnik: Sättigungsfunktionen
Praktische Hinweise
  • Tanh(0) = 0: Symmetriezentrum der Funktion
  • Beschränkt: -1 < Tanh(x) < 1 für alle x
  • Für große |x|: Tanh(x) ≈ ±1 · (1 - 2e^(-2|x|))
  • Für kleine |x|: Tanh(x) ≈ x (lineare Näherung)

Berechnungsbeispiele

Kleine Werte

Tanh(0) = 0

Tanh(0.5) ≈ 0.462

Tanh(1) ≈ 0.762

Mittlere Werte

Tanh(2) ≈ 0.964

Tanh(3) ≈ 0.995

Tanh(-2) ≈ -0.964

Grenzwerte

x → +∞: Tanh(x) → 1

x → -∞: Tanh(x) → -1

Niemals exakt ±1

Anwendungen in künstlicher Intelligenz

Neuronale Netze

Aktivierungsfunktion:

y = tanh(wx + b)

Nichtlineare Transformation

Vorteil: Symmetrisch um 0, steile Gradientenübergänge.

Signalverarbeitung

Sättigungsfunktion:

Beschränkt Ausgangssignale

Verhindert Übersteuerung

Anwendung: Adaptive Filter, Regelungssysteme.

Wichtige mathematische Beziehungen

Beziehung zu anderen hyperbolischen Funktionen
\[\tanh(x) = \frac{\sinh(x)}{\cosh(x)}\] \[\sech^2(x) = 1 - \tanh^2(x)\]

Identitäten: Fundamentale hyperbolische Beziehungen.

Integrale und Reihen
\[\int \tanh(x) dx = \ln(\cosh(x)) + C\] \[\tanh(x) = \sum_{n=1}^{\infty} \frac{B_{2n} 2^{2n} (2^{2n}-1)}{(2n)!} x^{2n-1}\]

Stammfunktion: Natürlicher Logarithmus von Cosh.


Informatik Funktionen

Dez-Hex-Bin-Oktal umwandeln • Bitweise schieben • Ein Bit setzen • Ein Bit zurücksetzen • Bitweise UND • Bitweise ODER • Bitweise exklusiv ODER

Spezial Funktionen

Airy • Abgeleitete Airy • Bessel I • Bessel Ie • Bessel J • Bessel Je • Bessel K • Bessel Ke • Bessel Y • Bessel Ye • Bessel Jv • Bessel Yv • Hankel • Beta • Unvollständige Beta • Inverse Unvollständige Beta • Binomialkoeffizient • Logarithmus des Binomialkoeffizienten • Erf • Erfc • Erfi • Erfci • Fibonacci • Fibonacci Tabelle • Gamma Funktion • Inverse Gamma • Log Gamma • Digamma • Trigamma • Logit • Sigmoid • Derivative Sigmoid • Softsign • Derivative Softsign • Softmax • Struve • Modifizierte Struve • Struve Tabelle • Modifizierte Struve Tabelle • Riemann Zeta

Hyperbolische Funktionen

ACosh • ACoth • ACsch • ASech • ASinh • ATanh • Cosh • Coth • Csch • Sech • Sinh • Tanh

Trigonometrische Funktionen

ACos • ACot • ACsc • ASec • ASin • ATan • Cos • Cot • Csc • Sec • Sin • Sinc • Tan • Grad in Radiant • Radiant in Grad