Inverse des hyperbolischen Tangens

Berechnung des Winkels zum inversen hyperbolischen Tangens

ATanh Rechner

Beschränkter Definitionsbereich

Die ATanh(x) oder inverse hyperbolische Tangens zeigt beschränktes Verhalten und ist nur für -1 < x < 1 definiert.

Eingabewert muss zwischen -1 und 1 liegen (-1 < x < 1)
Resultat
Winkel:

ATanh Funktionskurve

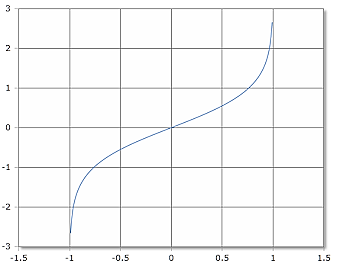
Kurve der ATanh Funktion

Die ATanh-Funktion ist nur für -1 < x < 1 definiert mit vertikalen Asymptoten bei x = ±1.
Definitionsbereich: (-1, 1), Wertebereich: ℝ

Beschränkter Definitionsbereich der ATanh-Funktion

Die inverse hyperbolische Tangens-Funktion hat einen kritisch beschränkten Definitionsbereich:

  • Definitionsbereich: -1 < x < 1 (offenes Intervall)
  • Wertebereich: ℝ (alle reellen Zahlen)
  • Asymptoten: Vertikale Asymptoten bei x = ±1
  • Monotonie: Streng monoton steigend
  • Symmetrie: Ungerade Funktion ATanh(-x) = -ATanh(x)
  • Bei x = ±1: ATanh(±1) → ±∞ (unendlich)

Logarithmische Darstellung der ATanh-Funktion

Die inverse hyperbolische Tangens-Funktion wird durch Logarithmus ausgedrückt:

Grundformel
\[\text{ATanh}(x) = \frac{1}{2} \ln \left( \frac{1+x}{1-x} \right)\]

Logarithmische Darstellung für -1 < x < 1

Umkehrrelation
\[\tanh(\text{ATanh}(x)) = x\]

Für -1 < x < 1

Formeln zur ATanh-Funktion

Definition
\[\text{ATanh}(x) = \frac{1}{2} \ln \left( \frac{1+x}{1-x} \right)\]

Fundamentale logarithmische Darstellung für -1 < x < 1

Umkehrrelation
\[\tanh(\text{ATanh}(x)) = x \quad \text{für } -1 < x < 1\]

Inverse Beziehung zum hyperbolischen Tangens

Ableitung
\[\frac{d}{dx} \text{ATanh}(x) = \frac{1}{1-x^2}\]

Erste Ableitung für -1 < x < 1

Symmetrieeigenschaft
\[\text{ATanh}(-x) = -\text{ATanh}(x)\]

Ungerade Funktion (antisymmetrisch)

Grenzwertverhalten
\[\lim_{x \to 1^-} \text{ATanh}(x) = +\infty\] \[\lim_{x \to -1^+} \text{ATanh}(x) = -\infty\]

Verhalten an den Asymptoten

Spezielle Werte

Wichtige Werte
ATanh(0) = 0 ATanh(0.5) ≈ 0.549 ATanh(-0.5) ≈ -0.549
Asymptoten
\[x = \pm 1: \text{ undefiniert}\]

Vertikale Asymptoten an diesen Stellen

Nullstelle
\[\text{ATanh}(0) = 0\]

Ursprungssymmetrie

Eigenschaften
  • Ungerade Funktion
  • Streng monoton steigend
  • Stetig im Definitionsbereich
  • Konvex für x > 0, konkav für x < 0
Anwendungen

Statistik (Logit-Transformation), Physik, hyperbolische Geometrie, Signalverarbeitung.

Ausführliche Beschreibung der ATanh-Funktion

Definition und Eingabe

Die inverse hyperbolische Tangens-Funktion ATanh(x) ist die Umkehrfunktion des hyperbolischen Tangens. Sie berechnet den Winkel, dessen hyperbolischer Tangens dem gegebenen Wert entspricht.

Kritische Bedingung: Das Argument muss -1 < x < 1 sein!
Eingabebeschränkung

Das Argument muss eine Zahl zwischen -1 und 1 sein. Bei einem Wert von -1 oder 1 wird als Resultat ∞ (unendlich) zurückgegeben. Bei anderen Werten außerhalb des Bereichs ist das Resultat NaN (keine gültige Nummer).

Verwendung des Rechners

Geben Sie einen Wert zwischen -1 und 1 ein (-1 < x < 1). Wählen Sie die gewünschte Maßeinheit (Grad oder Radiant) und die Anzahl der Dezimalstellen.

Resultat

Das Resultat wird in Grad (Vollkreis = 360°) oder Radiant (Vollkreis = 2π) angegeben. Die verwendete Maßeinheit wird mit dem entsprechenden Menü eingestellt.

Mathematische Eigenschaften

Funktionseigenschaften
  • Definitionsbereich: (-1, 1) (offenes Intervall)
  • Wertebereich: ℝ (alle reellen Zahlen)
  • Asymptoten: Vertikale Asymptoten bei x = ±1
  • Monotonie: Streng monoton steigend
Symmetrie und Verhalten
  • Ungerade Funktion: ATanh(-x) = -ATanh(x)
  • Nullstelle bei x = 0: ATanh(0) = 0
  • Wendepunkt im Ursprung
  • S-förmiger Kurvenverlauf
Anwendungen
  • Statistik: Logit-Transformation (Fisher-Z)
  • Physik: Relativistische Geschwindigkeiten
  • Signalverarbeitung: Hyperbolic wavelet
  • Neuronale Netze: Aktivierungsfunktionen
Praktische Hinweise
  • ATanh(0) = 0: Symmetriezentrum der Funktion
  • Beziehung: ATanh(x) = ½ ln((1+x)/(1-x))
  • Für |x| nahe 1: Funktion wächst sehr schnell
  • Ableitung: 1/(1-x²) divergiert bei x = ±1

Berechnungsbeispiele

Positive Werte

ATanh(0.5) ≈ 0.549

ATanh(0.9) ≈ 1.472

ATanh(0.99) ≈ 2.647

Negative Werte

ATanh(-0.5) ≈ -0.549

ATanh(-0.9) ≈ -1.472

ATanh(-0.99) ≈ -2.647

Grenzverhalten

x → 1⁻: ATanh(x) → +∞

x → -1⁺: ATanh(x) → -∞

ATanh(0) = 0


Informatik Funktionen

Dez-Hex-Bin-Oktal umwandeln • Bitweise schieben • Ein Bit setzen • Ein Bit zurücksetzen • Bitweise UND • Bitweise ODER • Bitweise exklusiv ODER

Spezial Funktionen

Airy • Abgeleitete Airy • Bessel I • Bessel Ie • Bessel J • Bessel Je • Bessel K • Bessel Ke • Bessel Y • Bessel Ye • Bessel Jv • Bessel Yv • Hankel • Beta • Unvollständige Beta • Inverse Unvollständige Beta • Binomialkoeffizient • Logarithmus des Binomialkoeffizienten • Erf • Erfc • Erfi • Erfci • Fibonacci • Fibonacci Tabelle • Gamma Funktion • Inverse Gamma • Log Gamma • Digamma • Trigamma • Logit • Sigmoid • Derivative Sigmoid • Softsign • Derivative Softsign • Softmax • Struve • Modifizierte Struve • Struve Tabelle • Modifizierte Struve Tabelle • Riemann Zeta

Hyperbolische Funktionen

ACosh • ACoth • ACsch • ASech • ASinh • ATanh • Cosh • Coth • Csch • Sech • Sinh • Tanh

Trigonometrische Funktionen

ACos • ACot • ACsc • ASec • ASin • ATan • Cos • Cot • Csc • Sec • Sin • Sinc • Tan • Grad in Radiant • Radiant in Grad