Sin - Sinus berechnen
Online Rechner zur Berechnung des Sinus eines Winkels
Sinus Rechner
Anleitung
Geben Sie den Winkel ein, dessen Sinus berechnet werden soll, wählen Sie die Maßeinheit (Grad oder Radiant) und klicken Sie auf Rechnen.
Sinus - Übersicht
Wertebereich
Der Winkel wird in Grad (Vollkreis = 360°) oder Radiant (Vollkreis = 2·π) angegeben. Das Resultat liegt immer im Bereich von -1 bis +1.
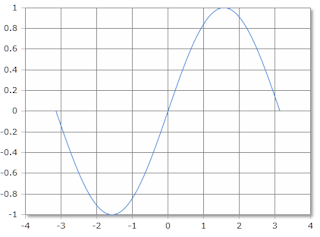
Sinus, Skala in Radiant
Definition im Dreieck
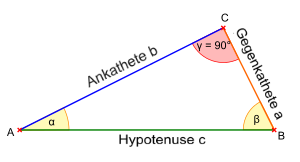
Der Sinus eines Winkels α entspricht dem Verhältnis der Gegenkathete zur Hypotenuse in einem rechtwinkligen Dreieck.
\(\displaystyle \sin(\alpha) = \frac{\text{Gegenkathete}}{\text{Hypotenuse}} = \frac{a}{c} \)
Wichtige Werte
- \( \sin(0°) = 0 \)
- \( \sin(30°) = 0.5 \)
- \( \sin(45°) = \frac{\sqrt{2}}{2} \approx 0.707 \)
- \( \sin(60°) = \frac{\sqrt{3}}{2} \approx 0.866 \)
- \( \sin(90°) = 1 \)
- \( \sin(180°) = 0 \)
|
|
Beschreibung zum Sinus
Grundlagen
Der Sinus ist eine der grundlegenden trigonometrischen Funktionen. In einem rechtwinkligen Dreieck ist der Sinus eines Winkels α das Verhältnis der Gegenkathete zur Hypotenuse.
Definition:
\(\displaystyle \sin(\alpha) = \frac{\text{Gegenkathete}}{\text{Hypotenuse}} \)
\(\displaystyle \sin(\alpha) = \frac{a}{c} \)
Eigenschaften
Die Sinusfunktion hat mehrere wichtige Eigenschaften:
- Periodisch: sin(α + 360°) = sin(α)
- Ungerade Funktion: sin(-α) = -sin(α)
- Wertebereich: -1 ≤ sin(α) ≤ 1
- Definitionsbereich: Alle reellen Zahlen
Beziehung zum Kosinus
Sinus und Kosinus sind eng miteinander verbunden:
\(\displaystyle \sin(\alpha) = \cos(90° - \alpha) \)
\(\displaystyle \sin^2(\alpha) + \cos^2(\alpha) = 1 \)
Detailliertes Beispiel
Beispiel 1: Sinus berechnen
Gegeben:
Ein rechtwinkliges Dreieck mit:
- Gegenkathete (zu α): \( a = 6 \text{ cm} \)
- Hypotenuse: \( c = 10 \text{ cm} \)
Berechnung:
\(\displaystyle \sin(\alpha) = \frac{6}{10} = 0.6 \)
Um den Winkel zu finden: \( \alpha = \arcsin(0.6) \approx 36.87° \)
Beispiel 2: Bekannte Winkel
Wichtige Sinuswerte:
| \( \sin(0°) \) | = | 0 |
| \( \sin(30°) \) | = | 0.5 |
| \( \sin(45°) \) | = | \( \frac{\sqrt{2}}{2} \approx 0.707 \) |
| \( \sin(60°) \) | = | \( \frac{\sqrt{3}}{2} \approx 0.866 \) |
| \( \sin(90°) \) | = | 1 |
| \( \sin(180°) \) | = | 0 |
Beispiel 3: Praktische Anwendung
Aufgabe:
Eine Leiter lehnt in einem Winkel von 30° an einer Wand. Die Leiter ist 8 m lang. Wie hoch reicht die Leiter an der Wand?
Lösung:
\(\displaystyle \text{Höhe} = 8 \cdot \sin(30°) = 8 \cdot 0.5 = 4 \text{ m} \)
Umrechnung
Von Grad zu Radiant:
\(\displaystyle \text{Radiant} = \frac{\text{Grad} \cdot \pi}{180°} \)
Mathematische Eigenschaften
- Periode: 360° bzw. 2π (Radiant)
- Symmetrie: Ungerade Funktion: sin(-α) = -sin(α)
- Nullstellen: Bei n·180° (n ganzzahlig)
- Extremwerte:
- Maximum: 1 bei 90°, 450°, ...
- Minimum: -1 bei 270°, 630°, ...
- Additionstheoreme:
- \( \sin(\alpha + \beta) = \sin\alpha\cos\beta + \cos\alpha\sin\beta \)
- \( \sin(\alpha - \beta) = \sin\alpha\cos\beta - \cos\alpha\sin\beta \)
Praktische Anwendungen
- Physik: Schwingungen und Wellen
- Navigation: Kursberechnungen und Positionsbestimmung
- Bauingenieurwesen: Höhenberechnungen und Neigungen
- Astronomie: Berechnung von Himmelspositionen
- Computergrafik: 3D-Rotationen und Animationen
- Elektrotechnik: Wechselstrom und Signalanalyse
- Maschinenbau: Bewegungsanalysen
- Vermessungswesen: Höhen- und Entfernungsbestimmung
Wichtiger Hinweis
Der Sinus ist eine periodische Funktion mit einer Periode von 360° bzw. 2π. Das bedeutet, dass sin(α) = sin(α + 360°) gilt. Der Wertebereich liegt immer zwischen -1 und +1, unabhängig vom Eingabewinkel. Die Sinusfunktion ist eine ungerade Funktion, d.h. punktsymmetrisch zum Ursprung: sin(-α) = -sin(α). Zusammen mit dem Kosinus erfüllt der Sinus die fundamentale trigonometrische Identität: sin²(α) + cos²(α) = 1, die als Pythagoreische Identität bekannt ist.
|
|