Hyperbolischer Kotangens

Berechnung des hyperbolischen Kotangens eines Winkels

Coth Rechner

Polstelle bei x = 0

Die Coth(x) oder hyperbolische Kotangens zeigt asymptotisches Verhalten mit einer Polstelle bei x = 0.

Winkel darf nicht 0 sein (x ≠ 0)
Resultat
Coth:

Coth Funktionskurve

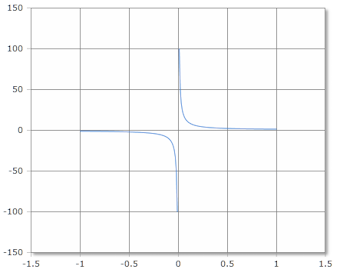
Kurve der Coth Funktion

Die Coth-Funktion hat eine Polstelle bei x = 0 und nähert sich asymptotisch ±1.
Definitionsbereich: ℝ \ {0}, Wertebereich: ℝ \ [-1, 1]

Polstelle und asymptotisches Verhalten der Coth-Funktion

Die hyperbolische Kotangens-Funktion zeigt charakteristische Diskontinuität:

  • Definitionsbereich: ℝ \ {0} (alle reellen Zahlen außer 0)
  • Wertebereich: ℝ \ [-1, 1] (außerhalb des Intervalls [-1, 1])
  • Polstelle: x = 0 (Singularität)
  • Asymptoten: Horizontale Asymptoten bei y = ±1
  • Symmetrie: Ungerade Funktion Coth(-x) = -Coth(x)
  • Monotonie: Streng monoton fallend in jedem Ast

Exponentialfunktion-Darstellung der Coth-Funktion

Die hyperbolische Kotangens-Funktion wird durch Exponentialfunktionen ausgedrückt:

Grundformel
\[\coth(x) = \frac{\cosh(x)}{\sinh(x)} = \frac{e^x + e^{-x}}{e^x - e^{-x}}\]

Verhältnis von Cosh zu Sinh für x ≠ 0

Alternative Form
\[\coth(x) = \frac{e^{2x} + 1}{e^{2x} - 1}\]

Vereinfachte Exponentialform

Formeln zur Coth-Funktion

Definition als Verhältnis
\[\coth(x) = \frac{\cosh(x)}{\sinh(x)}\]

Verhältnis von hyperbolischem Kosinus zu hyperbolischem Sinus

Exponentialform
\[\coth(x) = \frac{e^x + e^{-x}}{e^x - e^{-x}} = \frac{e^{2x} + 1}{e^{2x} - 1}\]

Direkte Exponentialfunktion-Darstellung für x ≠ 0

Ableitung
\[\frac{d}{dx} \coth(x) = -\csch^2(x) = -\frac{1}{\sinh^2(x)}\]

Erste Ableitung für x ≠ 0

Symmetrieeigenschaft
\[\coth(-x) = -\coth(x)\]

Ungerade Funktion (antisymmetrisch)

Grenzwertverhalten
\[\lim_{x \to 0^+} \coth(x) = +\infty\] \[\lim_{x \to 0^-} \coth(x) = -\infty\] \[\lim_{x \to \pm\infty} \coth(x) = \pm 1\]

Verhalten an Polstelle und asymptotisch

Spezielle Werte

Wichtige Werte
Coth(1) ≈ 1.313 Coth(-1) ≈ -1.313 Coth(2) ≈ 1.037
Polstelle
\[x = 0: \text{ undefiniert}\]

Vertikale Asymptote bei x = 0

Asymptoten
\[y = 1 \text{ für } x \to +\infty\] \[y = -1 \text{ für } x \to -\infty\]

Horizontale Asymptoten

Eigenschaften
  • Ungerade Funktion
  • Streng monoton fallend in jedem Ast
  • Zwei getrennte Äste
  • Horizontale Asymptoten bei y = ±1
Anwendungen

Langevin-Funktion, statistische Mechanik, Magnetismus, hyperbolische Geometrie.

Ausführliche Beschreibung der Coth-Funktion

Definition und Eingabe

Die hyperbolische Kotangens-Funktion Coth(x) ist eine mathematische Funktion aus der Familie der Hyperbelfunktionen. Sie wird definiert als das Verhältnis von hyperbolischem Kosinus zu hyperbolischem Sinus.

Kritische Eigenschaft: Die Coth-Funktion hat eine Polstelle bei x = 0!
Eingabe

Der Winkel wird in Grad (Vollkreis = 360°) oder Radiant (Vollkreis = 2π) angegeben. Die verwendete Maßeinheit wird mit dem Menü Grad oder Radiant eingestellt. Wichtig: Der Winkel darf nicht 0 sein!

Verwendung des Rechners

Geben Sie einen Winkel ungleich 0 ein. Bei x = 0 ist die Funktion nicht definiert! Wählen Sie die gewünschte Maßeinheit (Grad oder Radiant) und die Anzahl der Dezimalstellen.

Resultat

Das Resultat liegt immer außerhalb des Intervalls [-1, 1]. Für positive x ist Coth(x) > 1, für negative x ist Coth(x) < -1. Die Funktion nähert sich asymptotisch den Werten ±1.

Mathematische Eigenschaften

Funktionseigenschaften
  • Definitionsbereich: ℝ \ {0} (alle reellen Zahlen außer 0)
  • Wertebereich: (-∞, -1) ∪ (1, ∞)
  • Polstelle: x = 0 (vertikale Asymptote)
  • Symmetrie: Ungerade Funktion Coth(-x) = -Coth(x)
Asymptotisches Verhalten
  • Horizontale Asymptoten bei y = 1 und y = -1
  • Vertikale Asymptote bei x = 0
  • Streng monoton fallend in jedem Ast
  • Zwei getrennte Äste für x > 0 und x < 0
Anwendungen
  • Statistische Mechanik: Langevin-Funktion
  • Magnetismus: Paramagnetische Suszeptibilität
  • Relativitätstheorie: Geschwindigkeits-Transformationen
  • Hyperbolische Geometrie: Winkelfunktionen
Praktische Hinweise
  • Polstelle bei x = 0: Funktion divergiert
  • Ungerade Funktion: Coth(-x) = -Coth(x)
  • Asymptoten: y = ±1 für x → ±∞
  • Beziehung: Coth(x) = 1/Tanh(x) für x ≠ 0

Berechnungsbeispiele

Positive Werte

Coth(1) ≈ 1.313

Coth(2) ≈ 1.037

Coth(5) ≈ 1.000

Negative Werte

Coth(-1) ≈ -1.313

Coth(-2) ≈ -1.037

Coth(-5) ≈ -1.000

Grenzverhalten

x → 0⁺: Coth(x) → +∞

x → 0⁻: Coth(x) → -∞

x → ±∞: Coth(x) → ±1

Physikalische Anwendungen

Langevin-Funktion in der Magnetismus

Paramagnetismus:

L(x) = coth(x) - 1/x

Magnetische Suszeptibilität

Anwendung: Beschreibung der Magnetisierung von Materialien.

Statistische Mechanik

Boltzmann-Verteilung:

⟨E⟩ = -∂/∂β ln Z

Thermodynamische Größen

Beispiel: Mittlere Energie in zweiniveausystemen.


Informatik Funktionen

Dez-Hex-Bin-Oktal umwandeln • Bitweise schieben • Ein Bit setzen • Ein Bit zurücksetzen • Bitweise UND • Bitweise ODER • Bitweise exklusiv ODER

Spezial Funktionen

Airy • Abgeleitete Airy • Bessel I • Bessel Ie • Bessel J • Bessel Je • Bessel K • Bessel Ke • Bessel Y • Bessel Ye • Bessel Jv • Bessel Yv • Hankel • Beta • Unvollständige Beta • Inverse Unvollständige Beta • Binomialkoeffizient • Logarithmus des Binomialkoeffizienten • Erf • Erfc • Erfi • Erfci • Fibonacci • Fibonacci Tabelle • Gamma Funktion • Inverse Gamma • Log Gamma • Digamma • Trigamma • Logit • Sigmoid • Derivative Sigmoid • Softsign • Derivative Softsign • Softmax • Struve • Modifizierte Struve • Struve Tabelle • Modifizierte Struve Tabelle • Riemann Zeta

Hyperbolische Funktionen

ACosh • ACoth • ACsch • ASech • ASinh • ATanh • Cosh • Coth • Csch • Sech • Sinh • Tanh

Trigonometrische Funktionen

ACos • ACot • ACsc • ASec • ASin • ATan • Cos • Cot • Csc • Sec • Sin • Sinc • Tan • Grad in Radiant • Radiant in Grad