ACot - Arkuskotangens (inverser Kotangens)
Online Rechner zur Berechnung des Winkels zum Kotangens
Arkuskotangens Rechner
Anleitung
Geben Sie den Wert des Kotangens ein, wählen Sie die Maßeinheit (Grad oder Radiant) und klicken Sie auf Rechnen.
Arkuskotangens - Übersicht
Wertebereich
Das Resultat wird in Grad (Bereich = 0° bis 180°) oder Bogenmaß/Radiant (Bereich = 0 bis π) angegeben.
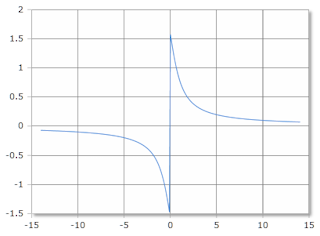
Inverser Kotangens, Skala in Radiant
Definition
Die inverse Kotangensfunktion (arccot, acot oder cot⁻¹) ist die Umkehrfunktion der Kotangens-Funktion. Sie berechnet den Winkel zu einem gegebenen Kotangenswert.
\(\displaystyle y = \text{arccot}(x) \Leftrightarrow \cot(y) = x \)
mit \( x \in \mathbb{R} \) und \( y \in (0, \pi) \) (Radiant)
Beziehung zum Tangens
Der Kotangens ist der Kehrwert des Tangens:
\(\displaystyle \cot(\alpha) = \frac{1}{\tan(\alpha)} = \frac{\cos(\alpha)}{\sin(\alpha)} \)
|
|
Beschreibung zum Arkuskotangens
Grundlagen
Die inverse Kotangensfunktion, bezeichnet als arccot, acot oder cot⁻¹, ist die Umkehrung der Kotangensfunktion. Sie wird verwendet, um den Winkel zu einem gegebenen Kotangenswert zu berechnen.
Mathematische Definition:
\(\displaystyle y = \text{arccot}(x) \)
bedeutet
\(\displaystyle \cot(y) = x \)
Kotangens im rechtwinkligen Dreieck
In einem rechtwinkligen Dreieck ist der Kotangens eines Winkels α das Verhältnis der Ankathete zur Gegenkathete:
\(\displaystyle \cot(\alpha) = \frac{\text{Ankathete}}{\text{Gegenkathete}} = \frac{b}{a} \)
\(\displaystyle \cot(\alpha) = \frac{\cos(\alpha)}{\sin(\alpha)} = \frac{1}{\tan(\alpha)} \)
Beziehung zum Tangens
Der Kotangens ist der Kehrwert des Tangens:
\(\displaystyle \cot(\alpha) = \frac{1}{\tan(\alpha)} \)
\(\displaystyle \tan(\alpha) = \frac{1}{\cot(\alpha)} \)
Detailliertes Beispiel
Beispiel 1: Kotangenswert berechnen
Gegeben:
Ein rechtwinkliges Dreieck mit:
- Ankathete: \( b = 8 \)
- Gegenkathete: \( a = 4 \)
Berechnung des Kotangens:
\(\displaystyle \cot(\alpha) = \frac{8}{4} = 2 \)
Beispiel 2: Winkel berechnen
Aufgabe:
Berechnen Sie den Winkel α für \( \cot(\alpha) = 2 \)
In Radiant:
\(\displaystyle \alpha = \text{arccot}(2) \approx 0.464 \text{ rad} \)
Umrechnung in Grad:
\(\displaystyle \alpha = \frac{0.464 \cdot 180°}{\pi} \approx 26.57° \)
Beispiel 3: Mit Tangens
Alternative Berechnung:
Da \( \cot(\alpha) = \frac{1}{\tan(\alpha)} \):
\(\displaystyle \tan(\alpha) = \frac{1}{2} = 0.5 \)
\(\displaystyle \alpha = \arctan(0.5) \approx 26.57° \)
Formel zur Umrechnung
Von Bogenmaß in Grad:
\(\displaystyle \text{Grad} = \frac{\text{Radiant} \cdot 180°}{\pi} \)
Eigenschaften
- Definitionsbereich: \( x \in \mathbb{R} \) (alle reellen Zahlen)
- Wertebereich: \( y \in (0, \pi) \) (Radiant) oder \( (0°, 180°) \)
- Monotonie: Streng monoton fallend
- Spezielle Werte:
- \( \text{arccot}(1) = \frac{\pi}{4} \approx 45° \)
- \( \text{arccot}(0) = \frac{\pi}{2} \approx 90° \)
- \( \text{arccot}(\infty) \to 0 \)
- \( \text{arccot}(-\infty) \to \pi \approx 180° \)
Praktische Anwendungen
- Geometrie: Winkelberechnung in rechtwinkligen Dreiecken
- Ingenieurwesen: Steigungswinkel und Neigungen
- Physik: Kräftezerlegung und Momentberechnungen
- Navigation: Peilungsberechnungen
- Computergrafik: Perspektivberechnungen
- Mathematik: Integralrechnung und komplexe Funktionen
Wichtige Formeln
Tangens und Kotangens:
\(\displaystyle \tan(\alpha) = \frac{\text{Gegenkathete}}{\text{Ankathete}} = \frac{a}{b} = \frac{\sin(\alpha)}{\cos(\alpha)} \)
\(\displaystyle \cot(\alpha) = \frac{\text{Ankathete}}{\text{Gegenkathete}} = \frac{b}{a} = \frac{\cos(\alpha)}{\sin(\alpha)} \)
Kehrwertbeziehung:
\(\displaystyle \cot(\alpha) = \frac{1}{\tan(\alpha)} \)
\(\displaystyle \tan(\alpha) = \frac{1}{\cot(\alpha)} \)
Wichtiger Hinweis
Die inverse Kotangensfunktion wird in Mathematik, Ingenieurwesen, Physik und Geometrie verwendet, um Winkel auf der Grundlage trigonometrischer Verhältnisse zu finden. Beachten Sie, dass der Kotangens der Kehrwert des Tangens ist, was alternative Berechnungsmethoden ermöglicht.
|
|