Cot - Kotangens berechnen
Online Rechner zur Berechnung des Kotangens eines Winkels
Kotangens Rechner
Anleitung
Geben Sie den Winkel ein (≠ 0°), dessen Kotangens berechnet werden soll, wählen Sie die Maßeinheit (Grad oder Radiant) und klicken Sie auf Rechnen.
Kotangens - Übersicht
Wichtiger Hinweis
Der Kotangens ist bei 0°, 180°, 360° etc. nicht definiert (Division durch Null). Der Wertebereich ist alle reellen Zahlen (von -∞ bis +∞).
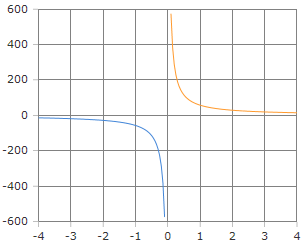
Kotangens, Skala in Grad
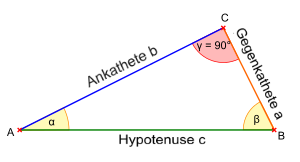
Definition im Dreieck
Der Kotangens ist der Kehrwert des Tangens und entspricht dem Verhältnis der Ankathete zur Gegenkathete.
\(\displaystyle \cot(\alpha) = \frac{\text{Ankathete}}{\text{Gegenkathete}} = \frac{b}{a} \)
\(\displaystyle \cot(\alpha) = \frac{1}{\tan(\alpha)} = \frac{\cos(\alpha)}{\sin(\alpha)} \)
Wichtige Werte
- \( \cot(30°) = \sqrt{3} \approx 1.732 \)
- \( \cot(45°) = 1 \)
- \( \cot(60°) = \frac{1}{\sqrt{3}} \approx 0.577 \)
- \( \cot(90°) = 0 \)
- \( \cot(0°) = \text{undefiniert} \) (∞)
|
|
Beschreibung zum Kotangens
Grundlagen
Der Kotangens ist eine trigonometrische Funktion und der Kehrwert des Tangens. In einem rechtwinkligen Dreieck ist der Kotangens eines Winkels α das Verhältnis der Ankathete zur Gegenkathete.
Definitionen:
\(\displaystyle \cot(\alpha) = \frac{\text{Ankathete}}{\text{Gegenkathete}} = \frac{b}{a} \)
\(\displaystyle \cot(\alpha) = \frac{1}{\tan(\alpha)} \)
\(\displaystyle \cot(\alpha) = \frac{\cos(\alpha)}{\sin(\alpha)} \)
Eigenschaften
Die Kotangensfunktion hat mehrere wichtige Eigenschaften:
- Periodisch: cot(α + 180°) = cot(α)
- Ungerade Funktion: cot(-α) = -cot(α)
- Wertebereich: Alle reellen Zahlen (-∞ bis +∞)
- Nullstellen: Bei 90° + n·180° (n ganzzahlig)
- Polstellen: Bei 0°, 180°, 360°, ... (nicht definiert)
Beziehung zu anderen Funktionen
Der Kotangens steht in enger Beziehung zu anderen trigonometrischen Funktionen:
\(\displaystyle \cot(\alpha) = \frac{1}{\tan(\alpha)} \)
\(\displaystyle \cot(\alpha) = \tan(90° - \alpha) \)
\(\displaystyle 1 + \cot^2(\alpha) = \csc^2(\alpha) \)
Detailliertes Beispiel
Beispiel 1: Kotangens berechnen
Gegeben:
Ein rechtwinkliges Dreieck mit:
- Ankathete (zu α): \( b = 6 \text{ cm} \)
- Gegenkathete: \( a = 4 \text{ cm} \)
Berechnung:
\(\displaystyle \cot(\alpha) = \frac{6}{4} = 1.5 \)
Um den Winkel zu finden: \( \alpha = \text{arccot}(1.5) \approx 33.69° \)
Beispiel 2: Bekannte Winkel
Wichtige Kotangenswerte:
| \( \cot(30°) \) | = | \( \sqrt{3} \approx 1.732 \) |
| \( \cot(45°) \) | = | 1 |
| \( \cot(60°) \) | = | \( \frac{1}{\sqrt{3}} \approx 0.577 \) |
| \( \cot(90°) \) | = | 0 |
| \( \cot(0°) \) | = | ∞ (undefiniert) |
| \( \cot(180°) \) | = | ∞ (undefiniert) |
Beispiel 3: Berechnung über Tangens
Aufgabe:
Berechnen Sie cot(30°) über den Tangens.
Lösung:
\(\displaystyle \tan(30°) \approx 0.577 \)
\(\displaystyle \cot(30°) = \frac{1}{\tan(30°)} = \frac{1}{0.577} \approx 1.732 \)
Umrechnung
Von Grad zu Radiant:
\(\displaystyle \text{Radiant} = \frac{\text{Grad} \cdot \pi}{180°} \)
Mathematische Eigenschaften
- Periode: 180° bzw. π (Radiant)
- Symmetrie: Ungerade Funktion: cot(-α) = -cot(α)
- Nullstellen: Bei 90° + n·180°
- Polstellen: Bei n·180° (n ganzzahlig)
- Grenzwerte:
- \( \lim_{\alpha \to 0^+} \cot(\alpha) = +\infty \)
- \( \lim_{\alpha \to 0^-} \cot(\alpha) = -\infty \)
- Identität: \( 1 + \cot^2(\alpha) = \csc^2(\alpha) \)
Praktische Anwendungen
- Geometrie: Winkelberechnungen in Dreiecken
- Vermessungswesen: Höhen- und Entfernungsberechnungen
- Physik: Analyse von Bewegungen und Kräften
- Navigation: Kurs- und Richtungsberechnungen
- Bauingenieurwesen: Neigungswinkel und Steigungen
- Optik: Strahlenberechnungen und Reflexionen
- Astronomie: Positionsbestimmungen
Wichtiger Hinweis
Der Kotangens ist der Kehrwert des Tangens und daher bei allen Winkeln nicht definiert, bei denen der Sinus Null ist (0°, 180°, 360° usw.). An diesen Stellen hat die Funktion Polstellen und strebt gegen ±∞. Der Kotangens hat eine Periode von 180° (bzw. π im Bogenmaß), was kürzer ist als die Periode von Sinus und Kosinus. Die Funktion ist eine ungerade Funktion, d.h. cot(-α) = -cot(α). Der Wertebereich umfasst alle reellen Zahlen von -∞ bis +∞.
|
|