ACos - Arkuskosinus (inverser Kosinus)
Online Rechner zur Berechnung des Winkels zum Kosinus
Arkuskosinus Rechner
Anleitung
Geben Sie den Wert des Kosinus ein (zwischen -1 und +1), wählen Sie die Maßeinheit (Grad oder Radiant) und klicken Sie auf Rechnen.
Arkuskosinus - Übersicht
Wertebereich
Der Wert des Arguments muss zwischen -1 und +1 liegen. Das Resultat wird in Grad (Vollkreis = 360°) oder Bogenmaß/Radiant (Vollkreis = 2 · π) angegeben.
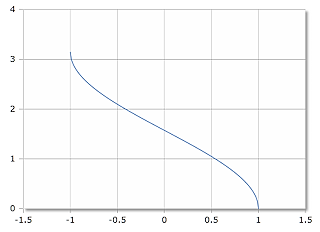
Inverser Kosinus, Skala in Radiant
Definition
Der Arkuskosinus (Arccos oder Acos) ist die Umkehrfunktion der Kosinus-Funktion. Sie berechnet den Winkel für einen gegebenen Kosinuswert.
\(\displaystyle y = \arccos(x) \Leftrightarrow \cos(y) = x \)
mit \( x \in [-1, 1] \) und \( y \in [0, \pi] \) (Radiant)
Umrechnung
Von Bogenmaß zu Grad:
\(\displaystyle \text{Grad} = \frac{\text{Radiant} \cdot 180°}{\pi} \)
|
|
Beschreibung zum Arkuskosinus
Grundlagen
Der Arkuskosinus (\( \arccos \) oder \( \text{acos} \)) ist die Umkehrfunktion der Kosinus-Funktion. Sie berechnet den Winkel für einen gegebenen Kosinuswert. Acos(x) gibt den zugehörigen Winkel in Bogenmaß zurück.
Mathematische Definition:
\(\displaystyle y = \arccos(x) \)
bedeutet
\(\displaystyle \cos(y) = x \)
Berechnung des Kosinuswerts
Der Kosinus ist eine trigonometrische Funktion, die sich auf ein rechtwinkliges Dreieck bezieht. In einem rechtwinkligen Dreieck ist der Kosinus eines Winkels α das Verhältnis der Länge der anliegenden Seite zur Hypotenuse:
\(\displaystyle \cos(\alpha) = \frac{\text{Anliegende Seite}}{\text{Hypotenuse}} \)
Wichtig: Der Kosinuswert liegt immer zwischen -1 und 1, und ein Winkel von 90 Grad hat einen Kosinuswert von 0.
Detailliertes Beispiel
Beispiel 1: Kosinuswert berechnen
Gegeben:
Ein rechtwinkliges Dreieck mit:
- Anliegende Seite: \( b = 6 \)
- Hypotenuse: \( c = 20 \)
Berechnung des Kosinus:
\(\displaystyle \cos(\alpha) = \frac{6}{20} = 0.3 \)
Beispiel 2: Winkel berechnen
Aufgabe:
Berechnen Sie den Winkel α für \( \cos(\alpha) = 0.3 \)
In Radiant:
\(\displaystyle \alpha = \arccos(0.3) \approx 1.266 \text{ rad} \)
Umrechnung in Grad:
\(\displaystyle \alpha = \frac{1.266 \cdot 180°}{\pi} \approx 72.54° \)
Formel zur Umrechnung
Von Bogenmaß in Grad:
\(\displaystyle \text{Grad} = \frac{\text{Radiant} \cdot 180°}{\pi} \)
Eigenschaften
- Definitionsbereich: \( x \in [-1, 1] \)
- Wertebereich: \( y \in [0, \pi] \) (Radiant) oder \( [0°, 180°] \)
- Monotonie: Streng monoton fallend
- Spezielle Werte:
- \( \arccos(1) = 0 \)
- \( \arccos(0) = \frac{\pi}{2} \approx 90° \)
- \( \arccos(-1) = \pi \approx 180° \)
Praktische Anwendungen
- Geometrie: Winkelberechnung in Dreiecken
- Navigation: Kursbestimmung und Positionierung
- Physik: Berechnung von Kraftwinkeln
- Computergrafik: 3D-Rotationen und Projektionen
- Robotik: Gelenkwinkelberechnungen
- Astronomie: Berechnung von Himmelskoordinaten
Wichtiger Hinweis
Beachten Sie die Notation: In der Programmierung werden die inversen trigonometrischen Funktionen oft mit den abgekürzten Formen asin, acos, atan aufgerufen. Die Notationen sin−1(x), cos−1(x), tan−1(x) können zu Verwirrung führen, da sie mit der Notation für die reziproken trigonometrischen Funktionen kollidieren.
|
|