Hyperbolischer Sinus

Berechnung des hyperbolischen Sinus eines Winkels

Sinh Rechner

Hyperbolische Funktion

Die Sinh(x) oder hyperbolische Sinus zeigt S-förmiges Verhalten und ist für alle reellen Zahlen definiert.

Winkel kann eine beliebige reelle Zahl sein
Resultat
Sinh:

Sinh Funktionskurve

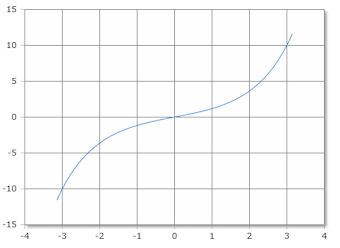
Kurve der Sinh Funktion

Die Sinh-Funktion ist S-förmig und streng monoton steigend für alle reellen Zahlen.
Definitionsbereich: ℝ, Wertebereich: ℝ

S-förmiges Verhalten der Sinh-Funktion

Die hyperbolische Sinus-Funktion zeigt charakteristische S-Kurven-Eigenschaften:

  • Definitionsbereich: ℝ (alle reellen Zahlen)
  • Wertebereich: ℝ (alle reellen Zahlen)
  • Nullstelle: Sinh(0) = 0
  • Symmetrie: Ungerade Funktion Sinh(-x) = -Sinh(x)
  • Monotonie: Streng monoton steigend
  • Wachstum: Exponentielles Wachstum für große |x|

Exponentialfunktion-Darstellung der Sinh-Funktion

Die hyperbolische Sinus-Funktion wird durch Exponentialfunktionen ausgedrückt:

Grundformel
\[\sinh(x) = \frac{e^x - e^{-x}}{2}\]

Exponentialfunktion-Darstellung für alle x ∈ ℝ

Umkehrrelation
\[\sinh(\text{ASinh}(x)) = x\]

Für alle x ∈ ℝ

Formeln zur Sinh-Funktion

Definition
\[\sinh(x) = \frac{e^x - e^{-x}}{2}\]

Fundamentale Exponentialfunktion-Darstellung für alle x ∈ ℝ

Identität mit Sinus
\[\sinh(ix) = i \sin(x)\]

Beziehung zum trigonometrischen Sinus (Euler-Formel)

Ableitung
\[\frac{d}{dx} \sinh(x) = \cosh(x)\]

Erste Ableitung ist der hyperbolische Kosinus

Additionstheorem
\[\sinh(x + y) = \sinh(x)\cosh(y) + \cosh(x)\sinh(y)\]

Hyperbolisches Additionstheorem

Hyperbolische Identität
\[\cosh^2(x) - \sinh^2(x) = 1\]

Fundamentale hyperbolische Identität (analog zu cos²-sin²=1)

Spezielle Werte

Wichtige Werte
Sinh(0) = 0 Sinh(1) ≈ 1.175 Sinh(-1) ≈ -1.175
Nullstelle
\[\sinh(0) = 0\]

Eindeutige Nullstelle im Ursprung

Eigenschaften
  • Ungerade Funktion
  • Streng monoton steigend
  • Überall stetig und differenzierbar
  • Exponentielles Wachstum für große |x|
Asymptotisches Verhalten
\[\sinh(x) \sim \frac{e^{|x|}}{2} \cdot \text{sign}(x) \]

Exponentielles Wachstum

Anwendungen

Relativitätstheorie, hyperbolische Geometrie, Ingenieurwesen, Kettenlinien-Probleme.

Ausführliche Beschreibung der Sinh-Funktion

Definition und Eingabe

Die hyperbolische Sinus-Funktion Sinh(x) ist eine ungerade und differenzierbare Funktion, die durch ihre Exponentialfunktion-Darstellung definiert ist.

Fundamentale Eigenschaft: Die Sinh-Funktion zeigt perfekte S-förmige Symmetrie!
Eingabe

Der Winkel wird in Grad (Vollkreis = 360°) oder Radiant (Vollkreis = 2π) angegeben. Die verwendete Maßeinheit wird mit dem Menü Grad oder Radiant eingestellt. Das Argument kann jede reelle Zahl sein.

Verwendung des Rechners

Geben Sie einen beliebigen Winkel ein. Es gibt keine Einschränkungen! Wählen Sie die gewünschte Maßeinheit (Grad oder Radiant) und die Anzahl der Dezimalstellen.

Resultat

Das Resultat kann sowohl positive als auch negative Werte annehmen. Die Funktion zeigt exponentielles Wachstum für große positive x und exponentiellen Abfall für große negative x.

Mathematische Eigenschaften

Funktionseigenschaften
  • Definitionsbereich: ℝ (alle reellen Zahlen)
  • Wertebereich: ℝ (alle reellen Zahlen)
  • Nullstelle: Sinh(0) = 0
  • Symmetrie: Ungerade Funktion Sinh(-x) = -Sinh(x)
S-Kurven-Eigenschaften
  • Perfekte S-förmige Kurve durch den Ursprung
  • Punktsymmetrisch zum Ursprung
  • Exponentiell wachsende Flanken
  • Wendepunkt im Ursprung
Anwendungen
  • Relativitätstheorie: Rapidität und Geschwindigkeiten
  • Hyperbolische Geometrie: Abstandsmessungen
  • Ingenieurwesen: Kabelformen und Hängestrukturen
  • Mathematische Physik: Wellengleichungen
Praktische Hinweise
  • Ungerade Funktion: Sinh(-x) = -Sinh(x)
  • Nullstelle bei x = 0: Sinh(0) = 0
  • Für große |x|: Sinh(x) ≈ (e^|x|/2)·sign(x)
  • Für kleine |x|: Sinh(x) ≈ x (lineare Näherung)

Berechnungsbeispiele

Positive Werte

Sinh(1) ≈ 1.175

Sinh(2) ≈ 3.627

Sinh(5) ≈ 74.203

Negative Werte

Sinh(-1) ≈ -1.175

Sinh(-2) ≈ -3.627

Sinh(-5) ≈ -74.203

Spezielle Werte

Sinh(0) = 0

Sinh(ln(2)) = 0.75

Sinh(π) ≈ 11.549

Physikalische Anwendungen

Relativitätstheorie

Rapidität:

φ = sinh⁻¹(v/c)

Relativistische Geschwindigkeiten

Anwendung: Lorentz-Transformationen, Teilchenphysik.

Wellengleichungen

Hyperbolische Wellen:

ψ(x,t) = A·sinh(kx - ωt)

Exponentiell wachsende Lösungen

Beispiel: Instabile Wellenmoden, Plasma-Physik.

Wichtige mathematische Beziehungen

Beziehung zu anderen hyperbolischen Funktionen
\[\tanh(x) = \frac{\sinh(x)}{\cosh(x)}\] \[\coth(x) = \frac{\cosh(x)}{\sinh(x)}\]

Identitäten: Fundamentale hyperbolische Beziehungen.

Integrale und Reihen
\[\int \sinh(x) dx = \cosh(x) + C\] \[\sinh(x) = \sum_{n=0}^{\infty} \frac{x^{2n+1}}{(2n+1)!}\]

Stammfunktion: Hyperbolischer Kosinus plus Konstante.


Informatik Funktionen

Dez-Hex-Bin-Oktal umwandeln • Bitweise schieben • Ein Bit setzen • Ein Bit zurücksetzen • Bitweise UND • Bitweise ODER • Bitweise exklusiv ODER

Spezial Funktionen

Airy • Abgeleitete Airy • Bessel I • Bessel Ie • Bessel J • Bessel Je • Bessel K • Bessel Ke • Bessel Y • Bessel Ye • Bessel Jv • Bessel Yv • Hankel • Beta • Unvollständige Beta • Inverse Unvollständige Beta • Binomialkoeffizient • Logarithmus des Binomialkoeffizienten • Erf • Erfc • Erfi • Erfci • Fibonacci • Fibonacci Tabelle • Gamma Funktion • Inverse Gamma • Log Gamma • Digamma • Trigamma • Logit • Sigmoid • Derivative Sigmoid • Softsign • Derivative Softsign • Softmax • Struve • Modifizierte Struve • Struve Tabelle • Modifizierte Struve Tabelle • Riemann Zeta

Hyperbolische Funktionen

ACosh • ACoth • ACsch • ASech • ASinh • ATanh • Cosh • Coth • Csch • Sech • Sinh • Tanh

Trigonometrische Funktionen

ACos • ACot • ACsc • ASec • ASin • ATan • Cos • Cot • Csc • Sec • Sin • Sinc • Tan • Grad in Radiant • Radiant in Grad